Предмет: Геометрия,
автор: Алиса9753
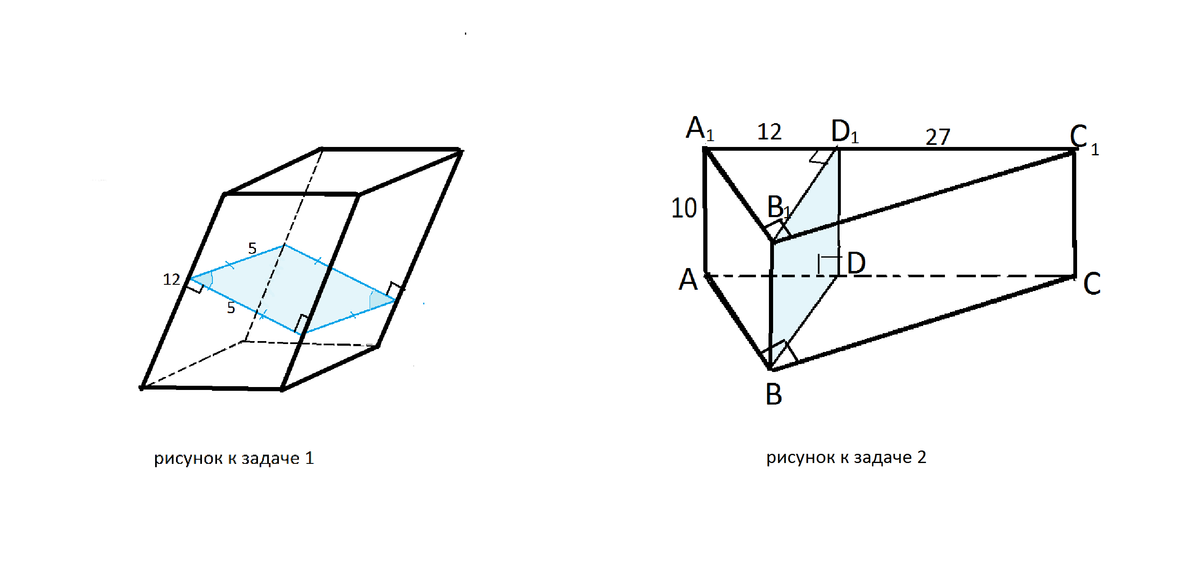
1) Боковое ребро наклонной четырёхугольной призмы равно 12 см, а перпендикулярным сечением является ромб со стороной 5 см. Найдите площадь боковой поверхности призмы.
2) Основанием прямой призмы АВСА1В1С1 является прямоугольный треугольник АВС с прямым углом В. Через ребро ВВ1 проведено сечение ВВ1D1D, перпендикулярное к плоскости грани АА1С1С. Найдите площадь сечения, если АА1= 10см, АD=27 см, DC=12см.
Ответы
Автор ответа:
0
1) Боковое ребро наклонной четырёхугольной призмы равно 12 см, а перпендикулярным сечением является ромб со стороной 5 см. Найдите площадь боковой поверхности призмы.
Каждая грань наклонной призмы - параллелограмм.
Площадь параллелограмма равна произведению высоты на сторону, к которой она проведена.
Так как сечением призмы является ромб ( стороны которого равны между собой), и сечение это перпендикулярно ребрам призмы, то стороны ромба - равные между собой высоты граней призмы.
Следовательно, все грани с равными сторонами (12 см) и высотами (5см)- равны.
Площадь боковой поверхности призмы равна учетверенной площади грани:
S бок= 4*5*12=240 см²
2) Основанием прямой призмы АВСА₁В₁С₁ является прямоугольный треугольник АВС с прямым углом В. Через ребро ВВ₁ проведено сечение ВВ₁D₁D, перпендикулярное к плоскости грани АА₁С₁С. Найдите площадь сечения, если АА₁= 10см, АD=27 см, DC=12см.
Грань АА₁С₁С содержит гипотенузы А₁С₁ верхнего и АС нижнего основания.
Сечение содержит высоты треугольников АВС и А₁В₁С₁.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Следовательно, ВD=В₁D₁ и
ВД=√АD·DС
ВD=√17·12=18 см
Площадь сечения - прямоугольника ВВ₁D₁D- равна произведению его сторон.
DD₁=АА₁=10 см по свойству ребер призмы
S ВВ₁D₁D=10·18=180 cм²
Каждая грань наклонной призмы - параллелограмм.
Площадь параллелограмма равна произведению высоты на сторону, к которой она проведена.
Так как сечением призмы является ромб ( стороны которого равны между собой), и сечение это перпендикулярно ребрам призмы, то стороны ромба - равные между собой высоты граней призмы.
Следовательно, все грани с равными сторонами (12 см) и высотами (5см)- равны.
Площадь боковой поверхности призмы равна учетверенной площади грани:
S бок= 4*5*12=240 см²
2) Основанием прямой призмы АВСА₁В₁С₁ является прямоугольный треугольник АВС с прямым углом В. Через ребро ВВ₁ проведено сечение ВВ₁D₁D, перпендикулярное к плоскости грани АА₁С₁С. Найдите площадь сечения, если АА₁= 10см, АD=27 см, DC=12см.
Грань АА₁С₁С содержит гипотенузы А₁С₁ верхнего и АС нижнего основания.
Сечение содержит высоты треугольников АВС и А₁В₁С₁.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Следовательно, ВD=В₁D₁ и
ВД=√АD·DС
ВD=√17·12=18 см
Площадь сечения - прямоугольника ВВ₁D₁D- равна произведению его сторон.
DD₁=АА₁=10 см по свойству ребер призмы
S ВВ₁D₁D=10·18=180 cм²
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Обществознание,
автор: 666butenko666daria66
Предмет: Алгебра,
автор: zaridzhaparova
Предмет: Алгебра,
автор: Дочурка
Предмет: Математика,
автор: 2002m