Предмет: Алгебра,
автор: nikulin96
Вычислить интегралы, пользуясь формулой Ньютона-Лейбница.
Приложения:
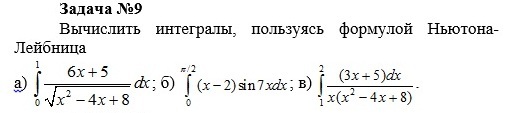
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: История,
автор: aishabairaihan
Предмет: Химия,
автор: anastasiafisanovic67
Предмет: Қазақ тiлi,
автор: anelomarova51
Предмет: Математика,
автор: 181212
Предмет: Обществознание,
автор: абвгдиеж