Question

В равнобедренной трапеции средняя линия равна 12 см, высота - 5 см. Найдите диагональ этой трапеции.

Answer 1

формула диагонали равнобедренной трапеции равна сумме квадратов высоты и средней линии (под корнем) 1) 12^2=144 2) 5^2=25 3) 144+25= 169 корень из 169 равен 13 Ответ: 13.

Answer 2

Один способ решения задачи дан в предыдущем решении.
Вариант решения 1)
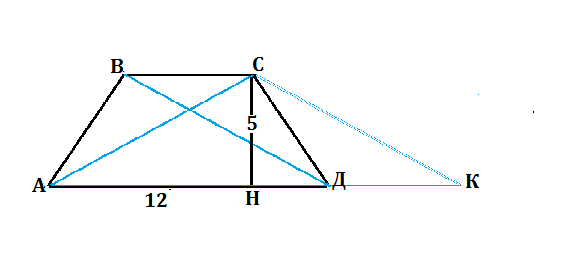
Высота равнобедренной трапеции, проведенная из тупого угла, делит большее основание на отрезки, один из которых равен полусумме оснований, другой - их полуразности. 
В трапеции АВСД отрезок АН равен полусумме оснований, т.е равен средней линии. 
В прямоугольном треугольнике АСН катет АН=12 см. СН=5 см,
 АС как гипотенуза треугольника из троек Пифагора равна 13 см. 
Проверим:
АС=√(12²+5²) =13 см
----
Вариант решения 2)
Диагонали равнобедренной трапеции равны. 
Если из вершины С провести прямую, параллельную диагонали ВД до пересечения с продолжением АД в точке К, получим равнобедренный треугольник АСК
ВСКД- параллелограмм, ДК=ВС
АК=АД+ВС=12*2=24,
СН высота и медиана треугольника АСК. 
АН=24:2=12
Из Δ АСН по т. Пифагора (см.выше)  АС=13