Предмет: Геометрия,
автор: Alex840
1. Осевое сечение цилиндра - квадрат, длина диагонали которого равна 36 см. Найдите радиус основания цилиндра.
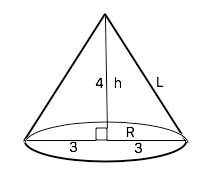
2. Радиус основания конуса равен 3м, а высота 4м. Найдите образующую, площадь полной поверхности конуса, площадь осевого сечения.
Ответы
Автор ответа:
0
1. Осевое сечение цилиндра - квадрат ⇒ диаметр основания равен высоте конуса, т.е. стороне этого квадрата. Диагональ делит квадрат на два равных прямоугольных с острыми углами 45°. Сторона квадрата (диаметр основания) равен 36•sin45°=36•1/√2=18√2 см. R=d:2=9√2 см .
2. Высота и радиус конуса – катеты прямоугольного (египетского) треугольника, его образующая – гипотенуза . R=d:2=3 м. ⇒ По т.Пифагора образующая L=√(4²+3²)=5 м. Осевое сечение конуса - равнобедренный треугольник. Ѕ(осев)=h•R=4•3=12м²
Ѕ(полн)=Ѕ(осн)+Ѕ(бок)
Ѕ(полн)=πR²+πRL=π3²+π•3•5=24π м²
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: ahan70025
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: зайчонок2