Предмет: Алгебра,
автор: astriddd
помогите, пожалуйста, решить уравнение!
Приложения:
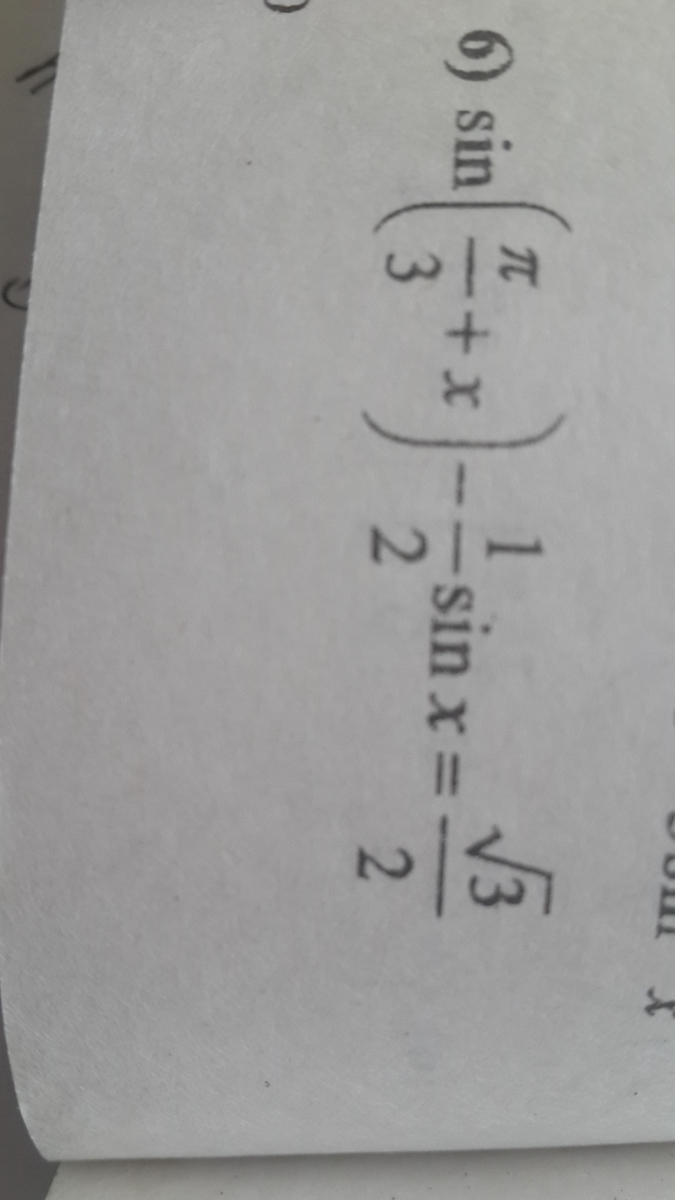
Ответы
Автор ответа:
0
sin(π/3+x)-(1/2)*sinx=√3/2
Используем формулу синус суммы sin(α+β)=sinαcosβ+cosαsinβ:
sin(π/3)*cosx+cos(π/3)*sinx-(1/2)*sinx=√3/2
(√3/2)*cosx+(1/2)*sinx-(1/2)*sinx=√3/2
(√3/2)*cosx=√3/2
cosx=1
x=2πn, n∈Z.
Используем формулу синус суммы sin(α+β)=sinαcosβ+cosαsinβ:
sin(π/3)*cosx+cos(π/3)*sinx-(1/2)*sinx=√3/2
(√3/2)*cosx+(1/2)*sinx-(1/2)*sinx=√3/2
(√3/2)*cosx=√3/2
cosx=1
x=2πn, n∈Z.
Похожие вопросы
Предмет: Математика,
автор: ibragimovam2109
Предмет: Математика,
автор: Аноним
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Геометрия,
автор: cheb8709