Предмет: Алгебра,
автор: sh04
если не затруднит, решите пожалуйста
Приложения:
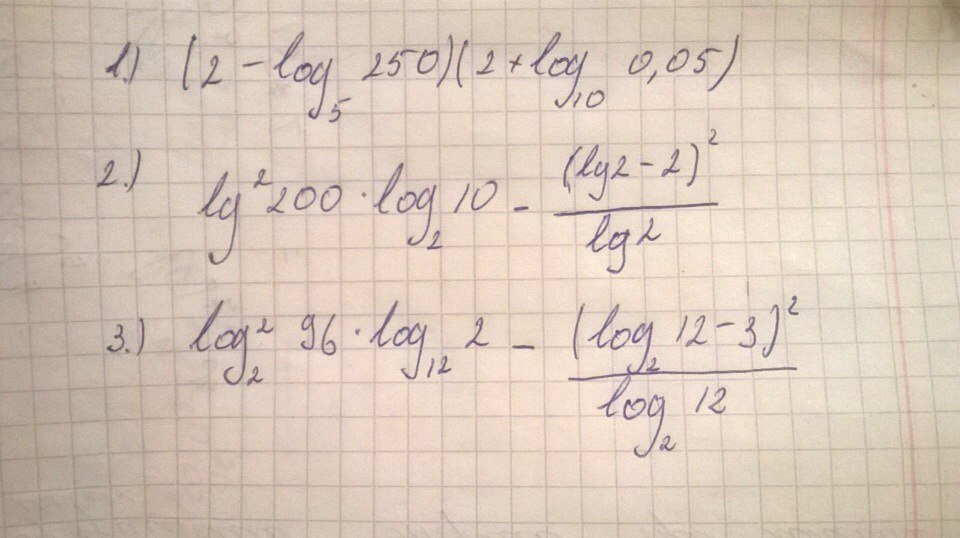
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Химия,
автор: slokunaleksa
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: zmuratova693
Предмет: Литература,
автор: sananika75
Предмет: Математика,
автор: encova