Предмет: Алгебра,
автор: Creator2000
Решить систему уравнений:
x^2y+xy^2=6
xy+(x+y)=5
Ответы
Автор ответа:
0
Вернемся к Х и У:
D = 4-12<0
Ответ: (2; 1); (1; 2).
Приложения:
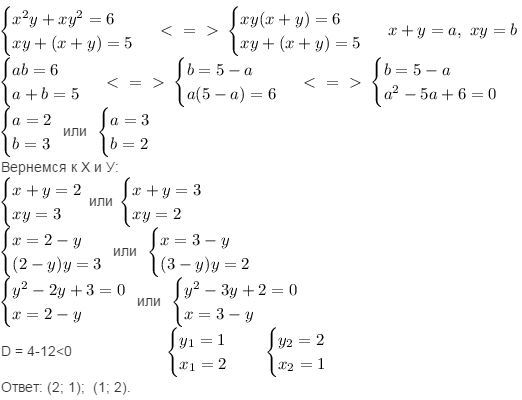
Похожие вопросы
Предмет: Биология,
автор: veronikaper125
Предмет: Математика,
автор: kausarkanatkyzy124
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: 11aknur08