Предмет: Геометрия,
автор: pyuol224
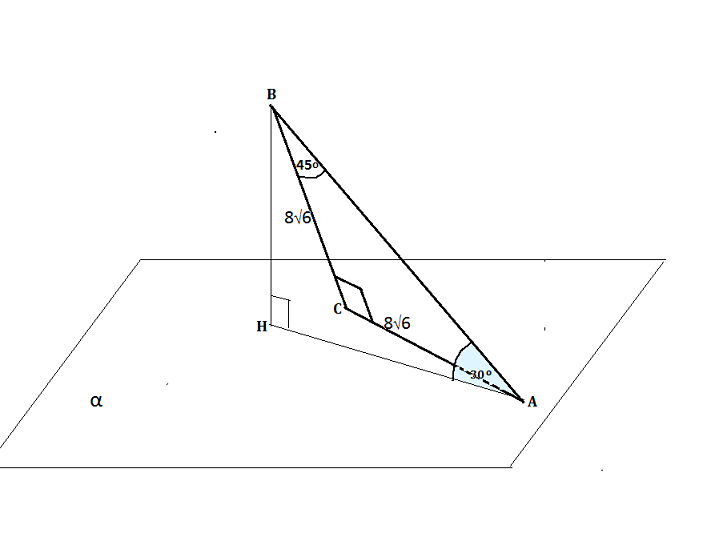
Треугольник ABC равнобедренный,AC=BC= 8sqrt{6} cм угол C= 90^{0} Плоскость a проходит через сторону AC причем сторона AB образует с плоскостью a угол 30^{0} Найдите расстояние от вершины B до плоскости a
Ответы
Автор ответа:
0
Угол между АВ и плоскостью α - это угол между АВ и ее проекцией АН на плоскость α
Т.к. треугольник АСВ прямоугольный равнобедренный, острые углы равны 45º
АВ=ВС:sin 45º=8√6:[(√2):2]=16√3
ВН - расстояние от В до плоскости α
ВН противолежит углу 30º и равен половине АВ.
ВН=8√3
Т.к. треугольник АСВ прямоугольный равнобедренный, острые углы равны 45º
АВ=ВС:sin 45º=8√6:[(√2):2]=16√3
ВН - расстояние от В до плоскости α
ВН противолежит углу 30º и равен половине АВ.
ВН=8√3
Приложения:
Похожие вопросы
Предмет: Литература,
автор: daniljoker8
Предмет: Физика,
автор: AbdulazizBrO000
Предмет: Қазақ тiлi,
автор: temirbekov5147685147
Предмет: Математика,
автор: енотина
Предмет: Литература,
автор: wiktorija1102