Предмет: Алгебра,
автор: aniyn
Решите, пожалуйста
Решить тригонометрические уравнения, картинка прилагается
Приложения:
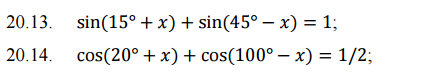
Ответы
Автор ответа:
0
20.13. sin(15 + x) + sin(45 - x) = 1
sin 15*cos x + cos 15*sin x + sin 45*cos x - cos 45*sin x = 1
cos x*(sin 15 + sin 45) + sin x*(cos 15 - cos 45) = 1
cos x*2sin 30*cos 15 + sin x*2sin 30*sin 15 = 1
sin 30 = 1/2, поэтому
cos x*cos 15 + sin x*sin 15 = cos (x - 15) = 1
x - 15 = 2pi*k = 360k
x = 15 + 360k
20.14.cos(20 + x) + cos(100 - x) = 1/2
cos 20*cos x - sin 20*sin x + cos 100*cos x + sin 100*sin x = 1/2
cos x*(cos 20 + cos 100) + sin x*(sin 100 - sin 20) = 1/2
cos x*2cos 60*cos 40 + sin x*2sin 40*cos 60 = 1/2
cos 60 = 1/2, поэтому
cos x*cos 40 + sin x*sin 40 = cos(x - 40) = 1/2
x1 - 40 = 60 + 360k; x1 = 100 + 360k
x2 - 40 = -60 + 360k; x2 = -20 + 360k
sin 15*cos x + cos 15*sin x + sin 45*cos x - cos 45*sin x = 1
cos x*(sin 15 + sin 45) + sin x*(cos 15 - cos 45) = 1
cos x*2sin 30*cos 15 + sin x*2sin 30*sin 15 = 1
sin 30 = 1/2, поэтому
cos x*cos 15 + sin x*sin 15 = cos (x - 15) = 1
x - 15 = 2pi*k = 360k
x = 15 + 360k
20.14.cos(20 + x) + cos(100 - x) = 1/2
cos 20*cos x - sin 20*sin x + cos 100*cos x + sin 100*sin x = 1/2
cos x*(cos 20 + cos 100) + sin x*(sin 100 - sin 20) = 1/2
cos x*2cos 60*cos 40 + sin x*2sin 40*cos 60 = 1/2
cos 60 = 1/2, поэтому
cos x*cos 40 + sin x*sin 40 = cos(x - 40) = 1/2
x1 - 40 = 60 + 360k; x1 = 100 + 360k
x2 - 40 = -60 + 360k; x2 = -20 + 360k
Похожие вопросы
Предмет: Математика,
автор: jantorereew
Предмет: Русский язык,
автор: nokiass159
Предмет: Другие предметы,
автор: RavilAkhmetov
Предмет: Математика,
автор: ghulienko85