Question

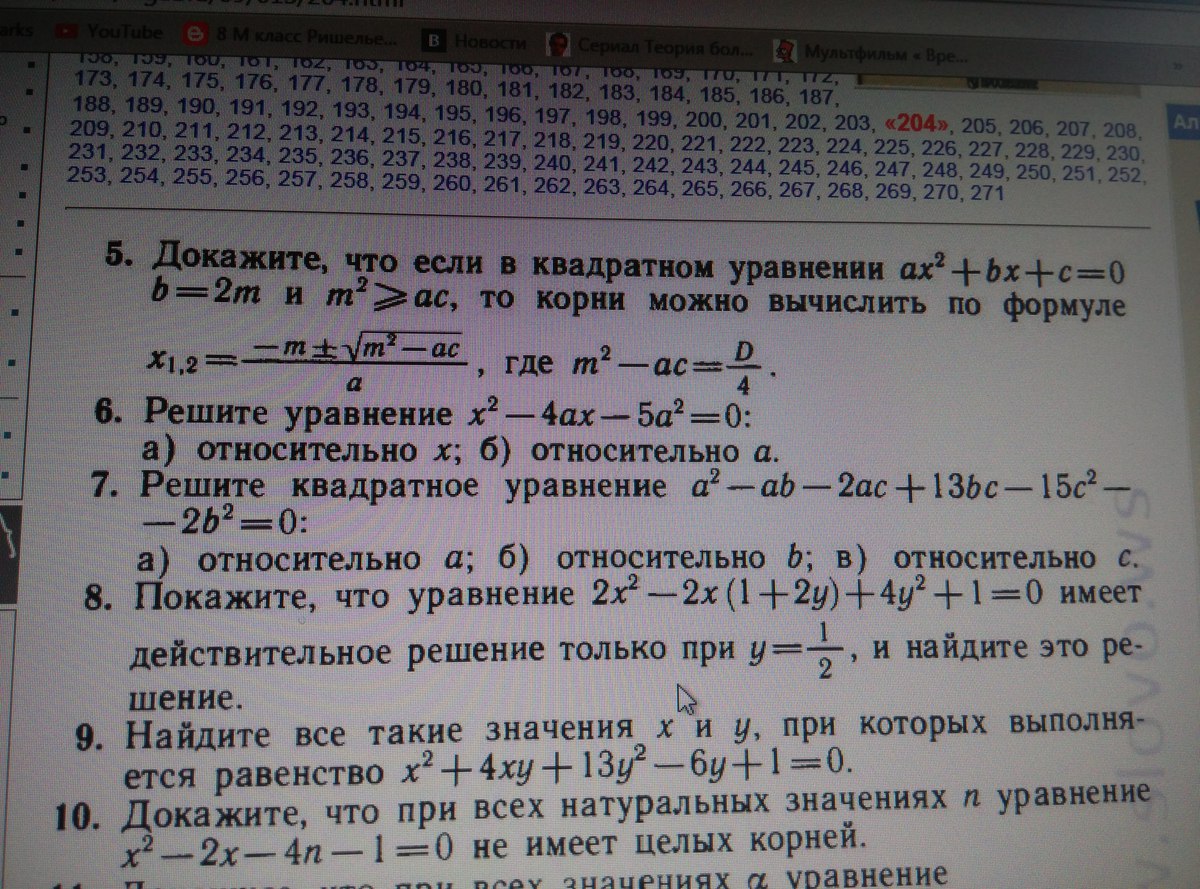
Докажите что если в квадратном уровнении ax^2+bx+c=0, b=2m и m^2>= ac, то корни можно вычислить по формуле x1,2 = (-m+-√m^2-ac)/a, где m^2-ac=D/4. Впрочем задача 5 на картинке . Решите пожалуйста!!

Answer 1

Если в квадратном уравнении коэффициент в=2m, то имеем дискриминант: D=(4m²-4ac) = 4(m²-ac). Тогда, если m²>ac, то уравнение имеет действительные корни по известной формуле:
Х1,2 = (-b±2√(b²-4ac ))/2а. Подставим b=2m и получим: Х1,2 = (-m±√(m²-ac ))/а, где  (m²-ac)=D/4.
Что и требовалось доказать.

Answer 2

спасибо)