Предмет: Математика,
автор: utilinaa
Помогите, пожалуйста. Буду очень благодарна
Приложения:
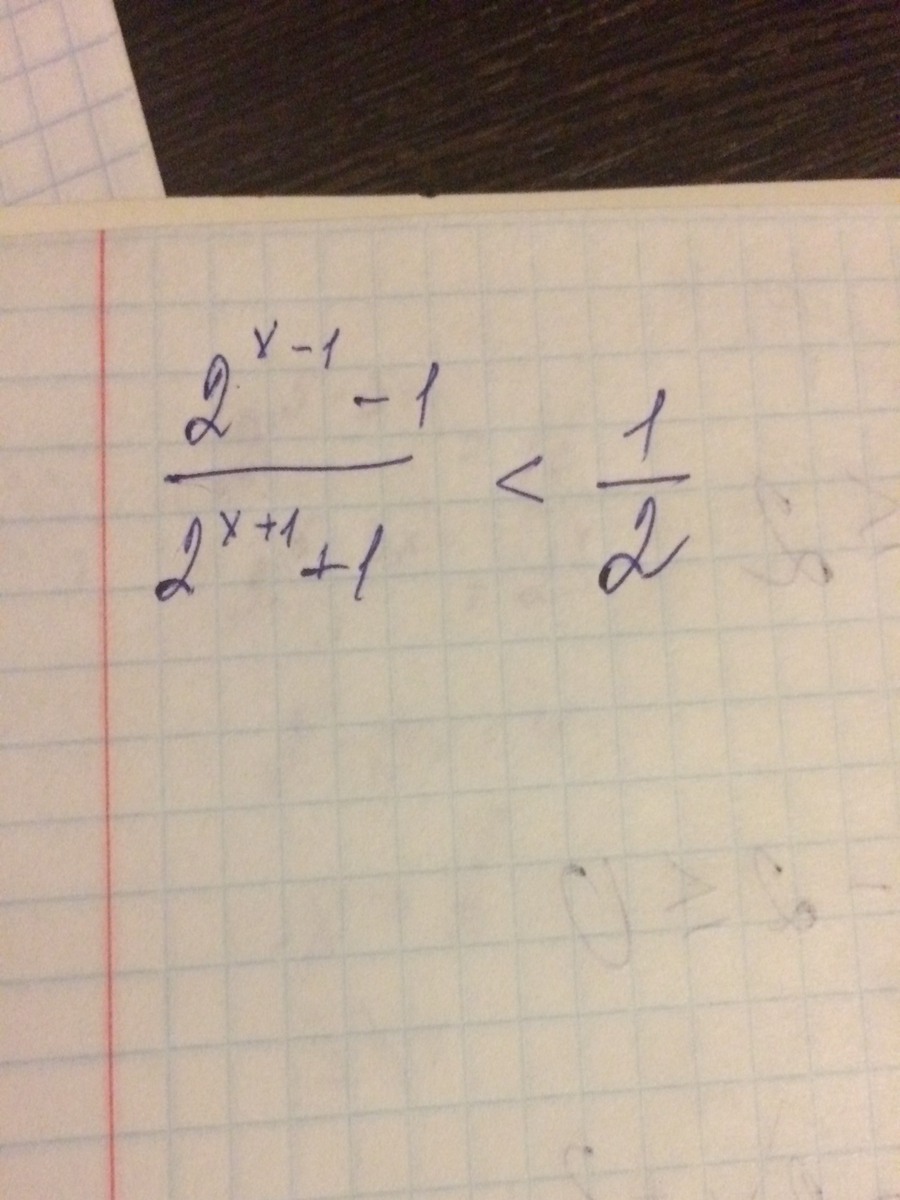
Ответы
Автор ответа:
0
Решим методом интервалов.
2^(x-1) - 1
⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻ - 1/2 <0
2^(x+1) +1
Рассмотрим функцию: у=2^(x-1) - 1
⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻ -1/2
2^(x+1) +1
Найдём область определения функции: D(x) =R
найдём нули функции:
2^(x-1) - 1
⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻ =1/2
2^(x+1) +1
2( 2^(x-1) - 1) = 2^(x+1) +1
2(2^x * 2⁻¹ -1) = 2^x * 2¹ + 1
2* 2^x * 1/2 - 2 = 2^x * 2¹ + 1
2^x -2 = 2^x * 2 +1
Пусть 2^x = t, t>0
t -2 = 2t +1
-t = 3
t=-3
корней нет
Определим знак функции: у(0) <0
Следовательно, неравенство верно при х∈(-∞; +∞)
2^(x-1) - 1
⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻ - 1/2 <0
2^(x+1) +1
Рассмотрим функцию: у=2^(x-1) - 1
⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻ -1/2
2^(x+1) +1
Найдём область определения функции: D(x) =R
найдём нули функции:
2^(x-1) - 1
⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻ =1/2
2^(x+1) +1
2( 2^(x-1) - 1) = 2^(x+1) +1
2(2^x * 2⁻¹ -1) = 2^x * 2¹ + 1
2* 2^x * 1/2 - 2 = 2^x * 2¹ + 1
2^x -2 = 2^x * 2 +1
Пусть 2^x = t, t>0
t -2 = 2t +1
-t = 3
t=-3
корней нет
Определим знак функции: у(0) <0
Следовательно, неравенство верно при х∈(-∞; +∞)
Автор ответа:
0
огромное вам спасибо!
Автор ответа:
0
извините, а почему приравнивается верхняя и нижняя часть? объясните, пожалуйста
Автор ответа:
0
и откуда взялась 2, которая выносится за скобку?
Похожие вопросы
Предмет: Русский язык,
автор: hodzaevdasi6
Предмет: Алгебра,
автор: oprad30
Предмет: География,
автор: ag8965749
Предмет: Химия,
автор: Ponca