Question

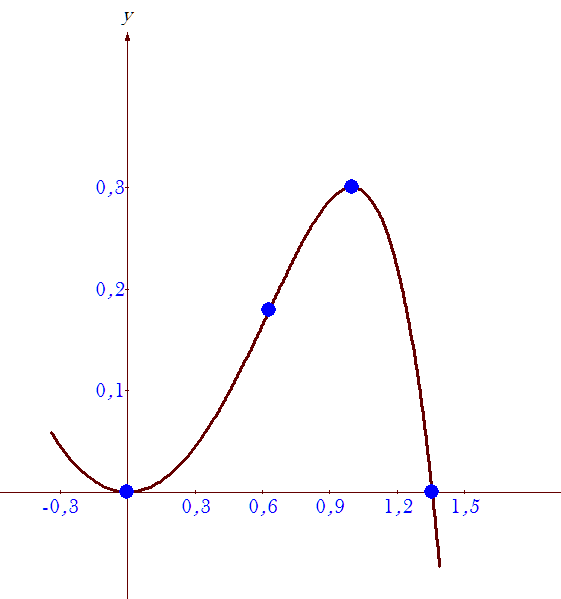
Исследуйте функцию и постройте график y=(1/2)*x^2-(1/5)*x^5

Answer 1

Исследуем заданную функцию $f(x)= frac{1}{2} x^2- frac{1}{5} x^5$
1. Область определения функции:
$D(f)=(-infty;+infty)$ - множество всех действительных чисел.
2. Четность функции
Функция $f:xrightarrow R$ называется четной, если выполняется равенство: 
$f(-x)=f(x)$, а нечётной - $f(-x)=-f(x)$
$f(-x)= frac{1}{2} (-x)^2- frac{1}{5} (-x)^5=-(- frac{1}{2} x^2- frac{1}{5} x^5)ne f(x)$
Итак, функция ни чётная ни нечётная.

3. Точки пересечения с осью Оу и Ох
 3.1. С осью Ох (f(x)=0), тоесть
$0,5x^2-0.2x^5=0\ x^2(0.5-0.2x^3)=0\ x_1=0;,,,,x_2= frac{ sqrt[3]{20} }{2}$
$(0;0),,( frac{ sqrt[3]{20} }{2} ;0)$ - точки пересечения с осью Ох
  3.2. С осью Оу (х=0)
Если х=0, то f(x)=0
(0;0) - точки пересечения с осью Оу

4. Критические точки, возрастание и убывание функции. Локальный максимум и локальный минимум.
 4.1. Найдем производную функции
$f'(x)=(0.5x^2-0.2x^5)'=(0.5x^2)'-(0.2x^5)'=x-x^4$
 Приравниваем производную функцию к нулю
$x-x^4=0;,,Rightarrow,, x(1-x^3)=0,,Rightarrow,,x_1=0,,,and,,,x_2=1$
____-__(0)____+____(1)___-_____
Функция возрастает на промежутке $(0;1)$, а убывает на промежутке - $(-infty;0)$ и $(1;+infty)$. В точке $x=0$ функция имеет локальный минимум, а в точке $x=1$ - локальный максимум
$(0;0)$ - относительный минимум, $(1;0.3)$ - относительный максимум

5. Точка перегиба.
 5.1. Вторая производная функции:
$f''(x)=(x-x^4)'=(x)'-(x^4)'=1-4x^3$
 Приравниваем ее к нулю
$1-4x^3=0;,,,Rightarrow,,,x= frac{ sqrt[3]{2} }{2}$
$f(frac{ sqrt[3]{2} }{2})=0.1125 sqrt[3]{4}$ - точка перегиба

Горизонтальных, наклонных и вертикальных асимптот нет.