Предмет: Алгебра,
автор: natalijirova
Привести к рациональному виду знаменатель дроби:
(x^2-2x)/(3-√(2x-1))
Ответы
Автор ответа:
0
Решение смотри в приложении
Приложения:
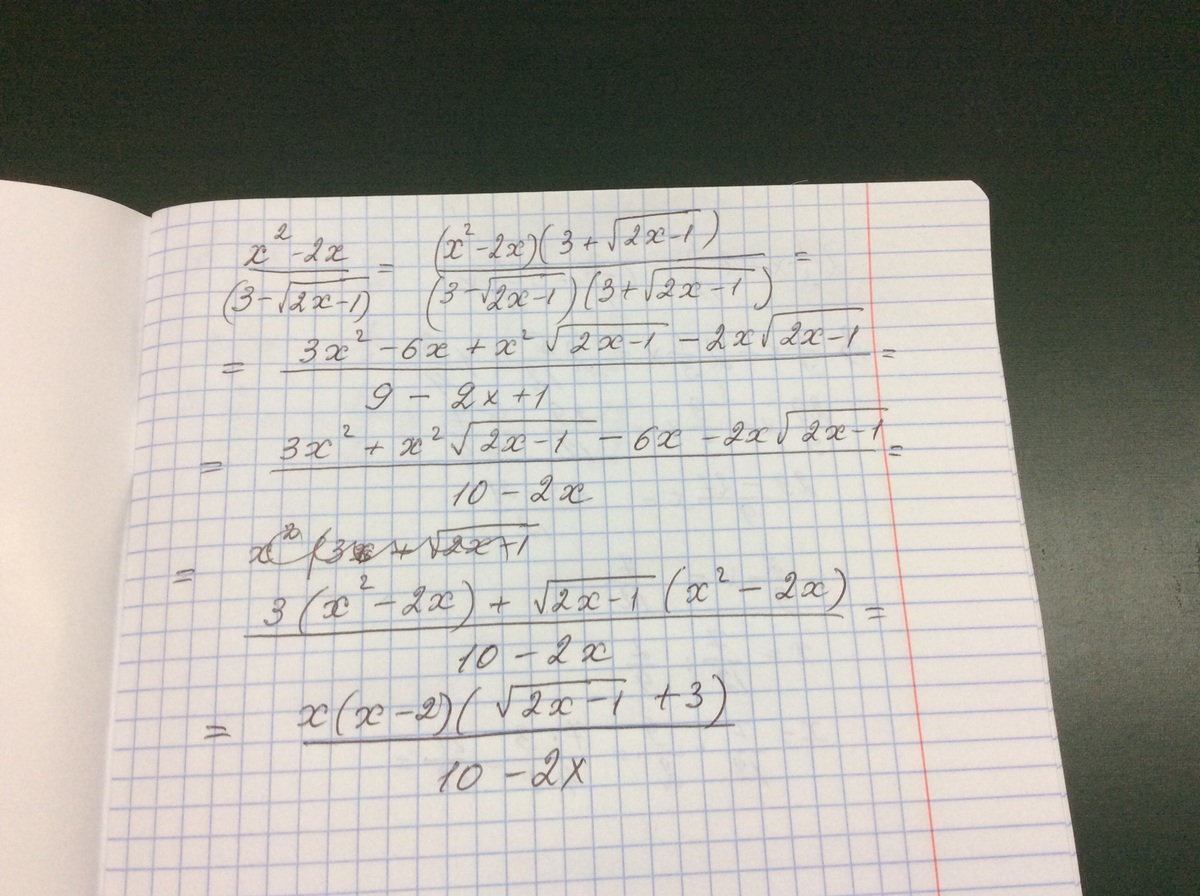
Автор ответа:
0
чтобы избавиться от иррациональности в знаменателе надо домножить и числитель и знаменатель на то же число, что и в знаменателе,(кроме нуля) но только с другим знаком (сопряженное число)
например: если в знаменателе (а-в), то нужно домножить на (а+в)
в данном выражении а=3, в=√(2x-1), тогда (x²-2x)/(3-√(2x-1)) нужно домножить на (3+√(2x+1)), получается
(x²-2x)/(3-√(2x-1))=(x²-2x)(3+√(2x+1))/(3-√(2x-1))(3+√(2x+1))=
(x²-2x)(3+√(2x+1))/(9-2х+1)=(x²-2x)(3+√(2x+1))/(10-2х)
можно также упростить:
х(x-2)(3+√(2x+1))/(10-2х)
например: если в знаменателе (а-в), то нужно домножить на (а+в)
в данном выражении а=3, в=√(2x-1), тогда (x²-2x)/(3-√(2x-1)) нужно домножить на (3+√(2x+1)), получается
(x²-2x)/(3-√(2x-1))=(x²-2x)(3+√(2x+1))/(3-√(2x-1))(3+√(2x+1))=
(x²-2x)(3+√(2x+1))/(9-2х+1)=(x²-2x)(3+√(2x+1))/(10-2х)
можно также упростить:
х(x-2)(3+√(2x+1))/(10-2х)
Приложения:
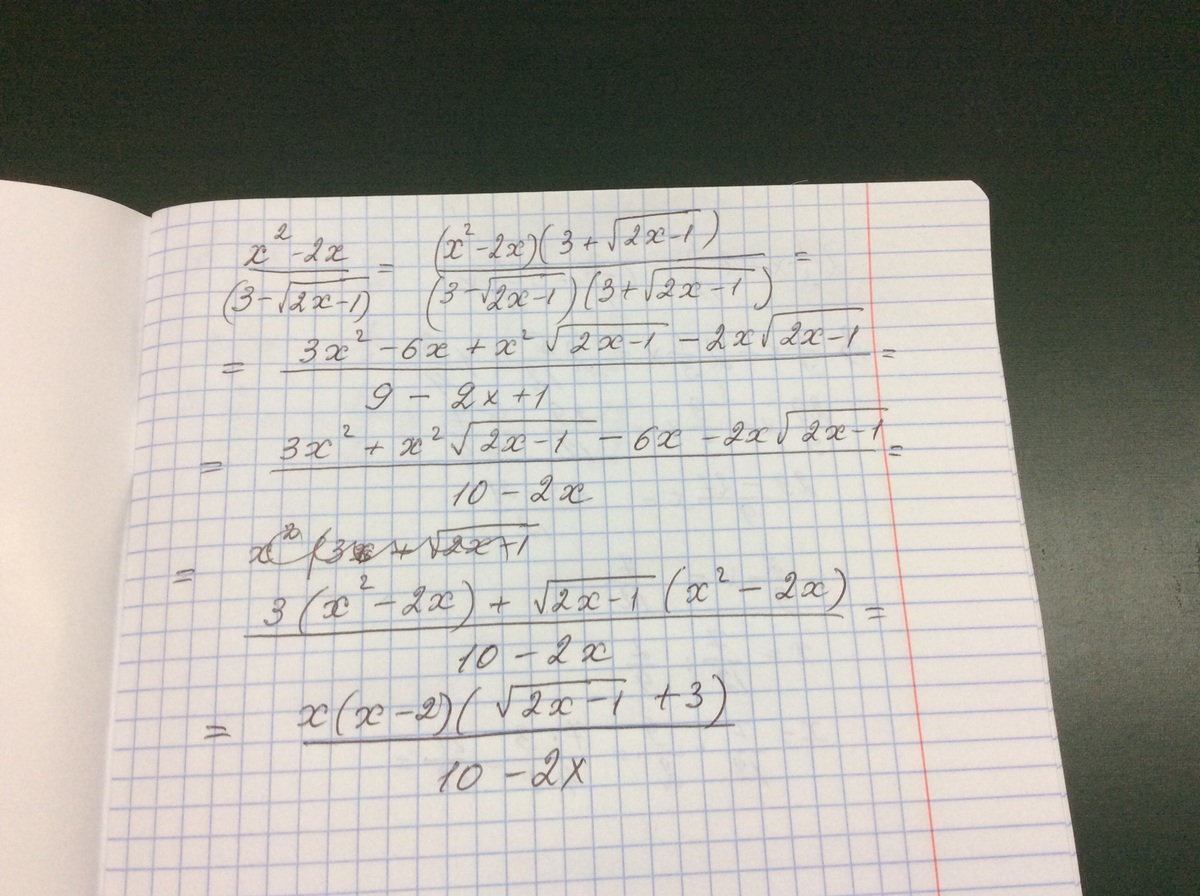
Похожие вопросы
Предмет: Математика,
автор: katerinaval174
Предмет: Музыка,
автор: shamilkurbanov2007
Предмет: Информатика,
автор: fonklove3
Предмет: Литература,
автор: KalinkaElena
Предмет: Алгебра,
автор: prosvirov97