Question

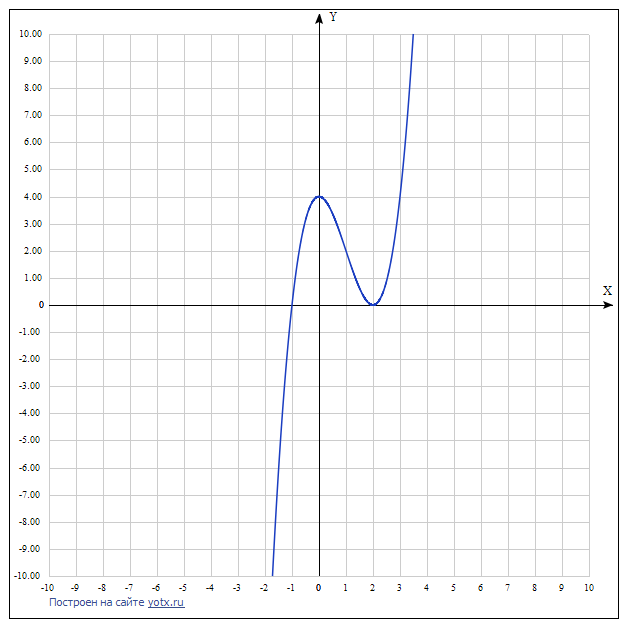
Исследуйте функцию f(х)=х^3-3х^2+4 И
Исследуйте функцию f(х)=х^3-3х^2+4
И постройте ее график ,заранее спасибо ,решается годовая оценка )

Число 12 представьте в виде суммы двух неотрицательных слагаемых так , что бы произведение квадрата одного из них на удвоенное другого слагаемого было наибольшим.

Answer 1

$y=f(x)=x^3-3x^2+4, \ 1)  D_y=R, \ 2)  E_y=R,$
$3)  f(-x)=(-x)^3-3(-x)^2+4=-x^3-3x^2+4=-(x^3+3x^2-4), \f(-x)neq f(x), \ f(-x)neq -f(x);$
функция общего вида (ни четная ни нечетная);
$4) x=0, f(0)=0^3-3cdot0^2+4=4, \ y=0, x^3-3x^2+4=0, \ x^3-2x^2-x^2+2x-2x+4=0, \ x^2(x-2)-x(x-2)-2(x-2)=0, \ (x-2)(x^2-x-2)=0, \ x-2=0, x_1=2, \ x^2-x-2=0, x_2=-1, x_3=2; \ (0;4), (-1;0), (2;0);$
нули функции;
$5) y=x^3-3x^2+4=(x+1)(x-2)^2, \ ygtrless0, (x+1)(x-2)^2gtrless0, \ (x-2)^2geq0 xin R, \ x+1gtrless0, \ xgtrless-1, \ x textless -1, xin(-infty;-1) y textless 0, \ x geq -1, xin[-1;+infty) y geq 0;$
промежутки знакопостоянства функции;
$6) f'(x)=(x^3-3x^2+4)'=3x^2-6x, \ f'(x)=0, 3x^2-6x=0, \ x(x-2)=0, \ x_1=0, x_2=2; \ f(0)=4, f(2)=0; \ (0;4), (2;0);$
критические точки функции;
$f'(x)gtrless0, 3x^2-6xgtrless0, \ x(x-2)gtrless0, \ x textless 0, xin(-infty;0) f'(x) textgreater 0 ynearrow, \ 0 textless x textless 2, xin(0;2) f'(x) textless 0 ysearrow, \ x textgreater 2, xin(2;+infty) f'(x) textgreater 0 ynearrow,$
промежутки возрастания и убывания функции;
$x_{max}=0, x_{min}=2, \ (0;4), (2;0);$
точки экстремумов;
$7) f''(x)=(3x^2-6x)'=6x-6, \ f''(x)=0, 6x-6=0, \ x=1, \ f(1)=1^3-3cdot1^2+4=2, \ (1;2)$
точка перегиба функции;
$f''(x)gtrless0, 6x-6gtrless0, \ xgtrless1, \ x textless 1, xin(-infty;1) f''(x) textless 0 yfrown, \ x textgreater 1, xin(1;+infty) f''(x) textgreater 0 ysmile;$
промежутки выпуклости вогнутости;
$8) limlimits_{x to +infty} f(x) = limlimits_{x to +infty} f(x) = limlimits_{x to +infty} x^3-3x^2+4 = +infty; \ limlimits_{x to -infty} f(x) = limlimits_{x to -infty} f(x) = limlimits_{x to -infty} x^3-3x^2+4 = -infty; \ x to +infty y to +infty, \ x to -infty y to -infty.$

x - одно из слагаемых, 12-х - второе слагаемое.
$x geq 0, 12-x geq 0, \ x leq 12, \ 0 leq x leq 12, xin[0;12]; \ p(x)=x^2cdot2(12-x)=2x^2(12-x), \ p'(x)=(2x^2(12-x))'=(24x^2-2x^3)'=48x-6x^2, \ p'(x)=0, 48x-6x^2=0, \ x(8-x)=0, \ x_1=0, x_2=8; \ p(0)=0^2cdot2(12-0)=0, \p(8)=8^2cdot2(12-8)=8^3=512, \ p(12)=12^2cdot2(12-12)=0, \ maxlimits_{xin[0;12]}2x^2(12-x) = 512, x=8; \ 12-x=4; \ 12=8+4.$