Question

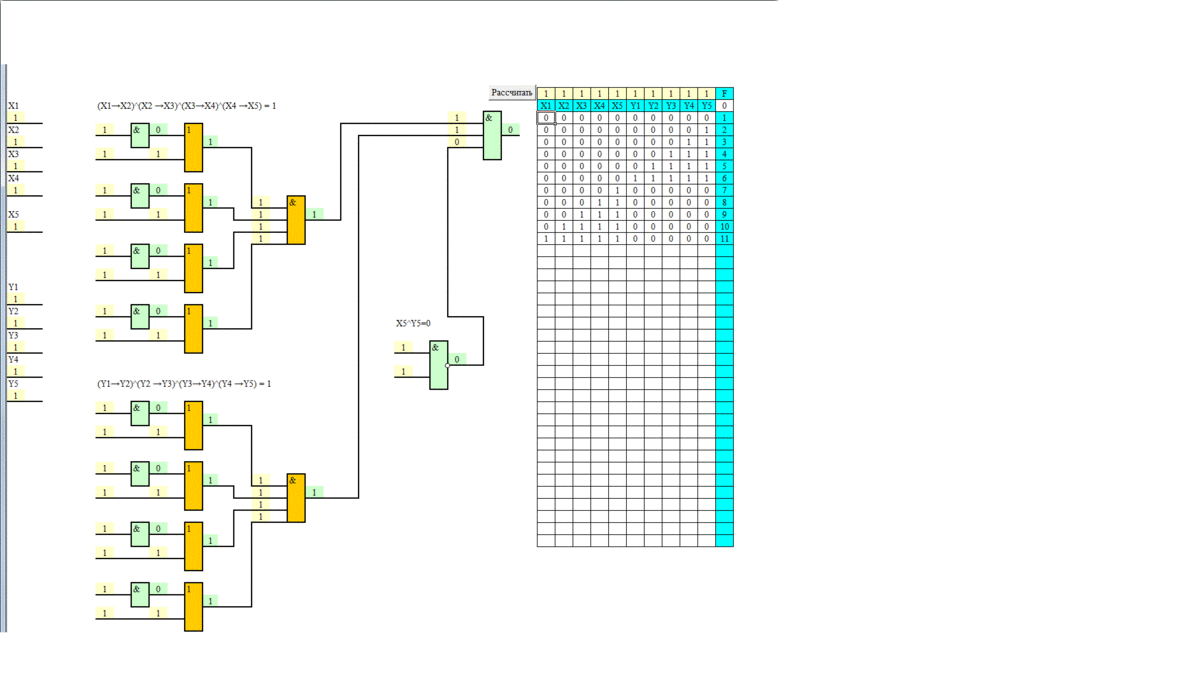
Сколько различных решений имеет система уравнений? (x1→x2)∧(x2→x3)∧(x3→x4)∧(x4→x5)=1 (у1→у2)∧(у2→у3)∧(у3→у4)∧(у4→у5)=1 x5∧у5=0 где x1,x2,…,x5,у1,у2,…,у5 – логические переменные. В качестве ответа нужно указать количество таких наборов.

Answer 1

Поправка: Всего 11 наборов.
см. приложения.
Лист Excel защищен без пароля, чтобы случайно не повредить формулы.
Снимаем пароль, копируем  элементы, получаем результат.
Программа в редакторе VBA

95dc974e8450699ea546497ddaa6df22.xls

Answer 2

попробуйте решить эту задачу

Answer 3

Сколько существует различных наборов значений логических переменных x1, x2,… x7, y1, y2,… y7, которые удовлетворяют всем перечисленным ниже условиям?
(x1=y1)→(x2=y2)
(x2=y2)→(x3=y3)
(x3=y3)→(x4=y4)
(x4=y4)→(x5=y5)
(x5=y5)→(x6=y6)
(x6=y6)→(x7=y7)В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать только количество таких наборов.

Answer 4

Нужно произвести замену: t1=(x1=y1)

Answer 5

получим t1->t2->t3->t4->t5->t6->t7 для t получится 7 решений=> 2^7*8=1024

Answer 6

большое спасибо!