Предмет: Алгебра,
автор: statova99
Буду очень благодарна! Пожалуйста!
Приложения:
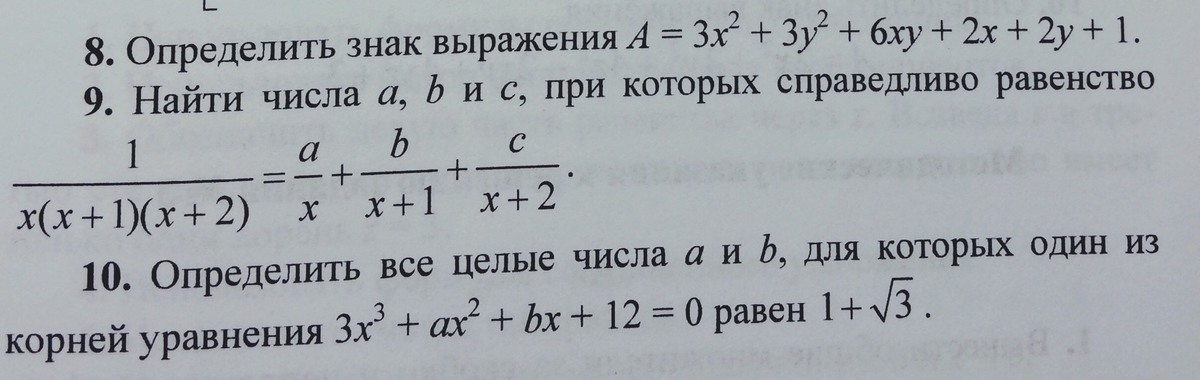
Ответы
Автор ответа:
0
8. A = 3x^2 + 3y^2 + 6xy + 2x + 2y + 1 =
= 3(x^2 + 2xy + y^2) + 2x + 2y + 1 = 3(x + y)^2 + 2(x + y) + 1 = 0
Получили квадратное уравнение относительно (x + y)
D = 2^2 - 4*3*1 = 4 - 12 = -8 < 0
Решений нет, оно всегда положительно.
9. Приводим правую часть к общему знаменателю


Коэффициенты при одинаковых степенях должны быть равны.
{ a + b + c = 0
{ 3a + 2b + c = 0
{ 2a = 1
Из 3 уравнения сразу a = 1/2, подставляем в 1 и 2 уравнения
{ 1/2 + b + c = 0
{ 3/2 + 2b + c = 0
Получаем
{ b + c = -1/2
{ 2b + c = -3/2
Из 2 уравнения вычитаем 1 уравнение
b = -3/2 + 1/2 = -1
Тогда c = -1/2 - b = -1/2 - (-1) = 1/2
Ответ:
10. Это просто - надо подставить x = 1+√3 в уравнение.





Свободное число и коэффициент при √3 должны оба равняться 0.
{ 30 + 4a + b + 12 = 0
{ 18 + 2a + b = 0
Из 1 уравнения вычитаем 2 уравнение
24 + 2a = 0
a = -12
b = -18 - 2a = -18 + 24 = 6
= 3(x^2 + 2xy + y^2) + 2x + 2y + 1 = 3(x + y)^2 + 2(x + y) + 1 = 0
Получили квадратное уравнение относительно (x + y)
D = 2^2 - 4*3*1 = 4 - 12 = -8 < 0
Решений нет, оно всегда положительно.
9. Приводим правую часть к общему знаменателю
Коэффициенты при одинаковых степенях должны быть равны.
{ a + b + c = 0
{ 3a + 2b + c = 0
{ 2a = 1
Из 3 уравнения сразу a = 1/2, подставляем в 1 и 2 уравнения
{ 1/2 + b + c = 0
{ 3/2 + 2b + c = 0
Получаем
{ b + c = -1/2
{ 2b + c = -3/2
Из 2 уравнения вычитаем 1 уравнение
b = -3/2 + 1/2 = -1
Тогда c = -1/2 - b = -1/2 - (-1) = 1/2
Ответ:
10. Это просто - надо подставить x = 1+√3 в уравнение.
Свободное число и коэффициент при √3 должны оба равняться 0.
{ 30 + 4a + b + 12 = 0
{ 18 + 2a + b = 0
Из 1 уравнения вычитаем 2 уравнение
24 + 2a = 0
a = -12
b = -18 - 2a = -18 + 24 = 6
Похожие вопросы
Предмет: География,
автор: 060508
Предмет: Русский язык,
автор: ola961
Предмет: Математика,
автор: Аноним
Предмет: Геометрия,
автор: vfksirfkbpf11
Предмет: Обществознание,
автор: VadimPozharskiy