Предмет: Математика,
автор: akav
Объясните, как найти множество решений неравенства:
log0.2((2x - 10)/(x + 11)) >= 0
Ответы
Автор ответа:
0
Приложения:
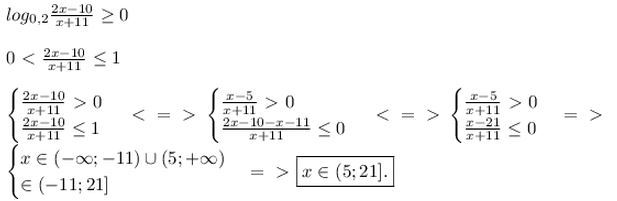
Похожие вопросы
Предмет: История,
автор: illiashkuleta
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Arseny338
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: Termit3008