Предмет: Алгебра,
автор: aikobiko
Найдите площадь треугольника, образованного прямой y=2-x, осью Ox и касательной, проведенной к графику y=1+2x-x^2 в точке x0=0. Спасибо
Ответы
Автор ответа:
0
1) Найдем уравнение касательной:






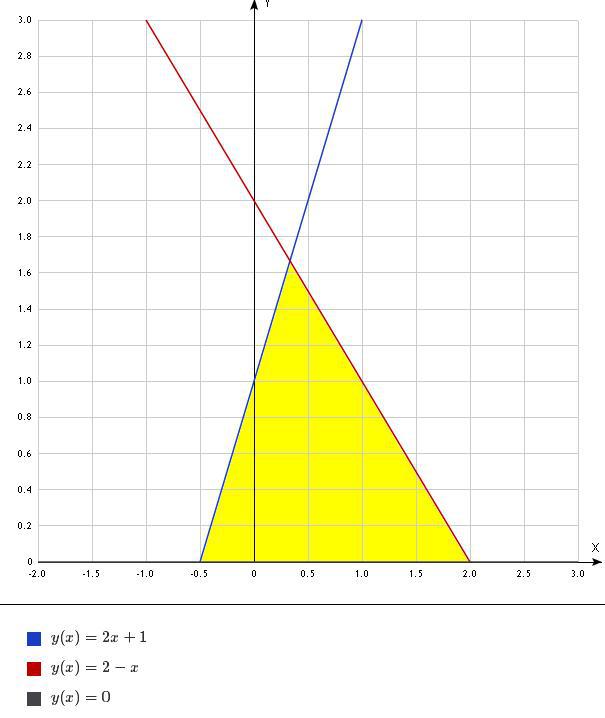
2) Начертим графики функций:



(см. рисунок, прикреплен)
3) Площадь фигуры найдем через интеграл. Для этого необходимо найти точки пересечения графиков:
3.1)


3.2)

3.3)

4) Площадь треугольника равна:

2) Начертим графики функций:
(см. рисунок, прикреплен)
3) Площадь фигуры найдем через интеграл. Для этого необходимо найти точки пересечения графиков:
3.1)
3.2)
3.3)
4) Площадь треугольника равна:
Приложения:
Автор ответа:
0
http://znanija.com/task/12672485
Автор ответа:
0
огромное спасибо за вашу помощь не поможете с этой задачей с условиями все порядке
Похожие вопросы
Предмет: Қазақ тiлi,
автор: volohovicalina
Предмет: Английский язык,
автор: mahanbetov2006
Предмет: История,
автор: alyonnaa
Предмет: Математика,
автор: niklana