Предмет: Математика,
автор: lithium95
Приложения определенного интеграла. Площадь фигуры
Приложения:
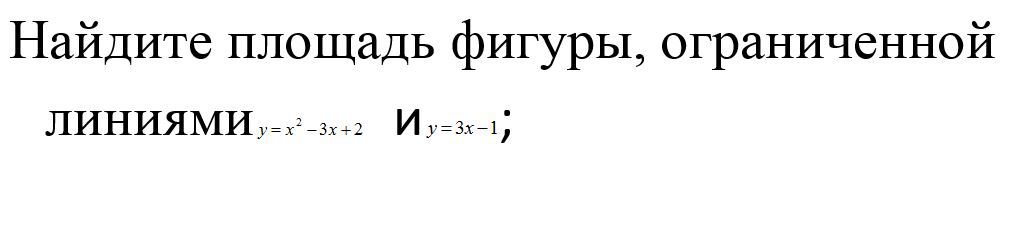
Ответы
Автор ответа:
0
Приложения:

Похожие вопросы
Предмет: Геометрия,
автор: mendal34
Предмет: Математика,
автор: Аноним
Предмет: Английский язык,
автор: alkeeva2006
Предмет: Литература,
автор: svetacvetochk