Предмет: Алгебра,
автор: aniyn
Решите,пожалуйста
Решить системы уравнений
Картинка прилагается
Приложения:
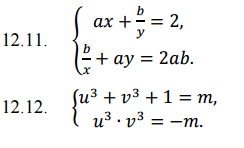
Ответы
Автор ответа:
0
12.11.

Замена 1/y=z



Получаем теорему Виета

Это значит, что переменные ax и bz являются корнями уравнения


Ответ: (1/a; b)
12.12.

Это сразу теорема Виета

Это значит, что переменные u^3 и v^3 являются корнями уравнения



![u1^{3} =-1;u1=-1; v1^{3} =m;v1= sqrt[3]{m} u1^{3} =-1;u1=-1; v1^{3} =m;v1= sqrt[3]{m}](https://tex.z-dn.net/?f=+u1%5E%7B3%7D+%3D-1%3Bu1%3D-1%3B+v1%5E%7B3%7D+%3Dm%3Bv1%3D+sqrt%5B3%5D%7Bm%7D+)
![u2^{3} =m;u2= sqrt[3]{m} ; v2^{3} =-1;v2=-1 u2^{3} =m;u2= sqrt[3]{m} ; v2^{3} =-1;v2=-1](https://tex.z-dn.net/?f=+u2%5E%7B3%7D+%3Dm%3Bu2%3D+sqrt%5B3%5D%7Bm%7D+%3B+v2%5E%7B3%7D+%3D-1%3Bv2%3D-1)
Ответ: (-1: кор.куб(m)); (кор.куб(m); -1)
Замена 1/y=z
Получаем теорему Виета
Это значит, что переменные ax и bz являются корнями уравнения
Ответ: (1/a; b)
12.12.
Это сразу теорема Виета
Это значит, что переменные u^3 и v^3 являются корнями уравнения
Ответ: (-1: кор.куб(m)); (кор.куб(m); -1)
Похожие вопросы
Предмет: Русский язык,
автор: rom4sergienko
Предмет: Русский язык,
автор: Plushenka2020
Предмет: Русский язык,
автор: kady45
Предмет: Биология,
автор: Alena1234567891