Предмет: Алгебра,
автор: mirasimashev
помогите решить задачу
Приложения:
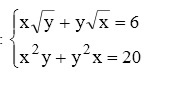
Ответы
Автор ответа:
0
Замена:
Замена:
Вернемся к замене:
1)
2)
Вернемся к замене:
1)
(1; 4)
2)
(4; 1)
Ответ: (1; 4), (4; 1)
Похожие вопросы
Предмет: Другие предметы,
автор: Helpanu13
Предмет: Математика,
автор: duapanpria
Предмет: Английский язык,
автор: vaskatya4905
Предмет: Математика,
автор: ViktoriaYkimova
Предмет: Математика,
автор: georkaziev