Предмет: Геометрия,
автор: amok033
В прямоугольном треугольнике гипотенуза равна 10 см,высота,проведенная из вершины прямого угла,равна 3 см.Найти отрезки на которые высота делит гипотенуза.
Ответы
Автор ответа:
0
Вариант решения.
Пусть АВС - данный треугольник с прямым углом В.
ВН - высота.
АН и НС - проекции катетов АВ и ВС на гипотенузу.
Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.⇒
АН²=АН*НС
Пусть АН=х, тогда
3²=х(10-х)⇒
х²-10х+9=0
Решив квадратное уравнение, получим.
х₁=9
х₂=1
Искомые отрезки равны 9 и 1.
-----------
В принципе, это то же решение, что при применении подобия треугольников АВН и СВН:
АН:ВН=ВН:СН
ВН²=АН*СН
и далее, как решено выше.
Пусть АВС - данный треугольник с прямым углом В.
ВН - высота.
АН и НС - проекции катетов АВ и ВС на гипотенузу.
Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.⇒
АН²=АН*НС
Пусть АН=х, тогда
3²=х(10-х)⇒
х²-10х+9=0
Решив квадратное уравнение, получим.
х₁=9
х₂=1
Искомые отрезки равны 9 и 1.
-----------
В принципе, это то же решение, что при применении подобия треугольников АВН и СВН:
АН:ВН=ВН:СН
ВН²=АН*СН
и далее, как решено выше.
Приложения:
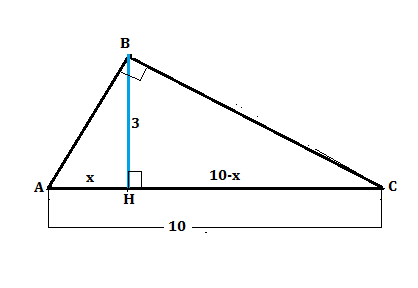
Похожие вопросы
Предмет: Литература,
автор: jamilyat94
Предмет: Қазақ тiлi,
автор: buller58
Предмет: Математика,
автор: omagarbldanilacrazy
Предмет: Литература,
автор: Risk14
Предмет: Математика,
автор: МаСяNя