Предмет: Математика,
автор: stasyaL
Помогите,пожалуйста! С решением,если можно)
Приложения:
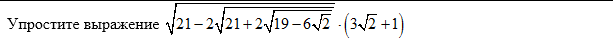
Ответы
Автор ответа:
0
Похожие вопросы