Предмет: Геометрия,
автор: Nurbi2001
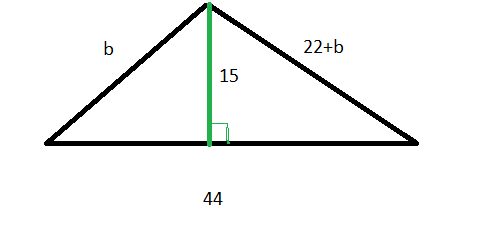
Помогите пожалуйста!!! в треугольнике АВС сторона с= 44, опущенная на нее из вершины С высота = 15, разность длин сторон а - в=22 . Чему равны стороны а и в ???
Ответы
Автор ответа:
0
См. обозначения на рисунке.
Применяем теорему Пифагора к двум прямоугольным треугольникам, образованным высотой и сторонами а и b


Возводим в квадрат при условии, что

Возводим в квадрат при условии, что 33-b≥0

D=22²-4·(-663)=3136=56²
b₁=(-22+56)/2=17 b₂<0 не удовлетворяет условию задачи
а=22+17=39
Ответ. а=39 b=17
Применяем теорему Пифагора к двум прямоугольным треугольникам, образованным высотой и сторонами а и b
Возводим в квадрат при условии, что
Возводим в квадрат при условии, что 33-b≥0
D=22²-4·(-663)=3136=56²
b₁=(-22+56)/2=17 b₂<0 не удовлетворяет условию задачи
а=22+17=39
Ответ. а=39 b=17
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: Аноним
Предмет: Русский язык,
автор: anekrasov1204
Предмет: Русский язык,
автор: rembekovdaniar
Предмет: Математика,
автор: belka281
Предмет: Биология,
автор: 55530125