Предмет: Геометрия,
автор: belikovada
Помогите решить!
Около равнобедренного треугольника АВС с основанием АВ и углом 120 градусов описана окружность. Докажите, что отрезок, соединяющий центр описанной окружности с точкой пересечения продолжения высот треугольника, равен диаметру описанной окружности.
Ответы
Автор ответа:
0
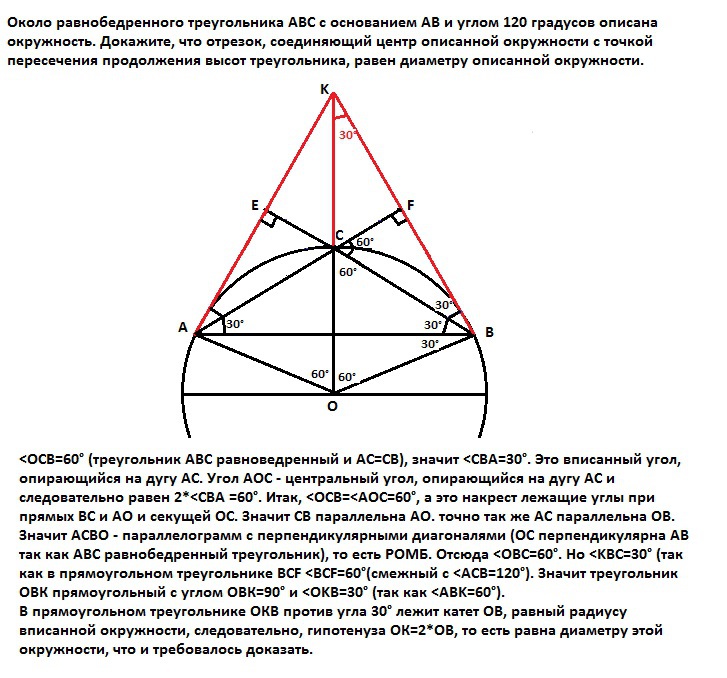
BF - высота к АС, АЕ - высота к ВС. Точка К - пересечение продолжений высот треугольника АВС.
<OCB=60° (треугольник АВС равноведренный и АС=СВ), значит <CBА=30°. Это вписанный угол, опирающийся на дугу АС. Угол АОС - центральный угол, опирающийся на дугу АС и следовательно равен 2*<CBА =60°. Итак, <OCB=<AOC=60°, а это накрест лежащие углы при прямых ВС и АО и секущей ОС. Значит СВ параллельна АО. точно так же АС параллельна
ОВ. Значит АСВО - параллелограмм с перпендикулярными диагоналями (ОС перпендикулярна АВ так как АВС равнобедренный треугольник), то есть РОМБ. Отсюда <OBC=60°. Но <KBC=30° (так как в прямоугольном треугольнике BCF <BCF=60°(смежный с <ACB=120°).
Значит треугольник ОВК прямоугольный с углом ОВК=90° и <OKB=30° (так как <ABK=60°). В прямоугольном треугольнике ОКВ против угла 30° лежит катет ОВ, равный радиусу вписанной окружности, следовательно, гипотенуза ОК=2*ОВ, то есть равна диаметру этой окружности, что и требовалось доказать.
<OCB=60° (треугольник АВС равноведренный и АС=СВ), значит <CBА=30°. Это вписанный угол, опирающийся на дугу АС. Угол АОС - центральный угол, опирающийся на дугу АС и следовательно равен 2*<CBА =60°. Итак, <OCB=<AOC=60°, а это накрест лежащие углы при прямых ВС и АО и секущей ОС. Значит СВ параллельна АО. точно так же АС параллельна
ОВ. Значит АСВО - параллелограмм с перпендикулярными диагоналями (ОС перпендикулярна АВ так как АВС равнобедренный треугольник), то есть РОМБ. Отсюда <OBC=60°. Но <KBC=30° (так как в прямоугольном треугольнике BCF <BCF=60°(смежный с <ACB=120°).
Значит треугольник ОВК прямоугольный с углом ОВК=90° и <OKB=30° (так как <ABK=60°). В прямоугольном треугольнике ОКВ против угла 30° лежит катет ОВ, равный радиусу вписанной окружности, следовательно, гипотенуза ОК=2*ОВ, то есть равна диаметру этой окружности, что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: sharovsd1807
Предмет: Геометрия,
автор: step31121981
Предмет: Алгебра,
автор: lyudmilaagisheva78
Предмет: Математика,
автор: varyaangel