Предмет: Алгебра,
автор: Julia34region
Помогите решить 5 и 6 номер пожалуйста.Второе фото - решала сама, но что-то не так...
Приложения:
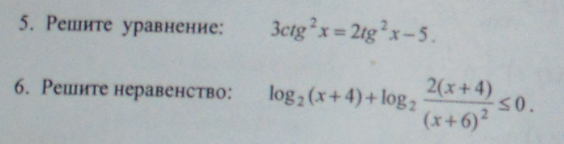

Ответы
Автор ответа:
0
или
это уравнение не имеет решений
Решаем первое:
2
ОДЗ:
х+4>0
x≠-6
Заменим сумму логарифмов логарифмом произведения
Можно умножить на положительное выражение (х+6)² (х≠-6)
обе части неравенства
2(x²+8x+16)≤x²+12x+36
x²+4x-4≤0
D=16+16=32
x₁=(-4-4√2)/2=-2-2√2 или x₂=(-4+4√2)/2=-2+2√2
+ - +
-----------[-2-2√2]------------------------[-2+2√2]---------------
\\\\\\\\\\\\\\\
C учетом ОДЗ получаем ответ
(-4; -2+2√2]
Автор ответа:
0
C 10 раза получилось тоже самое.Спасибо!
Автор ответа:
0
Ну получилось же! и это здОрово! Задачки -то непростые
Похожие вопросы
Предмет: Русский язык,
автор: abdyjaparovbakay
Предмет: Математика,
автор: denya5628
Предмет: Литература,
автор: polin4caz
Предмет: Математика,
автор: Марина0215
Предмет: Химия,
автор: Akashi21