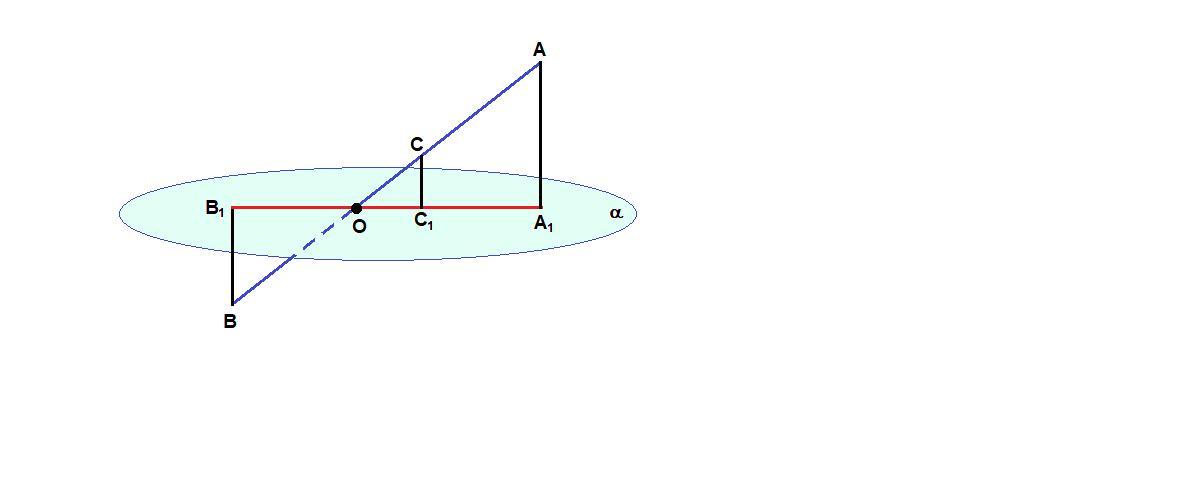
Концы отрезка АВ расположены по разные стороны от плоскости а. Точка С принадлежит АВ и АС :СВ=2:3. Через точки А,В,С проведены параллельные прямые, которые пресекают плоскость а в точках А,В,С1. Найдите длину отрезка СС1, если АА1=8 см и ВВ1=3см
Ответы
Ответ:
СС₁ = 3,6 см
Объяснение:
Через параллельные прямые АА₁ и ВВ₁ проходит плоскость, которая пересекает плоскость α по прямой А₁В₁. Значит и прямая СС₁, параллельная прямой АА₁, лежит в этой плоскости, т.е. точка С₁ лежит на прямой А₁В₁.
ΔАА₁О подобен ΔВВ₁О по двум углам (углы при вершине О равны как вертикальные, ∠А₁АО = ∠В₁ВО как накрест лежащие при пересечении АА₁║ВВ₁ секущей АВ).
АО : ВО = АА₁ : ВВ₁ = 8 : 3
Выразим все отрезки, как части от отрезка АВ.
АО - 8 частей, ВО - 3 части, значит
АО = 8/11 АВ
ВО = 3/11 АВ
АС : СВ = 2 : 3
АС - 2 части, СВ - 3 части, значит
АС = 2/5 АВ,
СВ = 3/5 АВ.
Тогда СО = АО - АС = 8/11 АВ - 2/5 АВ = 40/55 АВ - 22/55 АВ =
= 18/55 АВ.
ΔСС₁О подобен ΔАА₁О по двум углам (угол при вершине О общий, ∠ОСС₁ = ∠ОАА₁ как соответственные при пересечении АА₁║СС₁ секущей АО)
СС₁ : АА₁ = ОС : АО = 18/55 АВ : (40/55 АВ) = 18 : 40 = 9 : 20
СС₁ = 9 · 8 / 20 = 3,6 см