Question

Помогите пожалуйста с последним номером,мне бы только объяснить,чтобы я расписать все могла. Спасибо заранее огромное

Answer 1

Квадратичная функция имеет вид

$y=ax^2+bx+c$

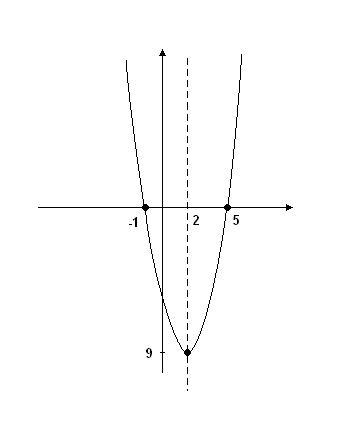
Графиком её является парабола. Наша парабола пересекает ось OX в точках (-1;0) и (5;0). То есть, удовлетворяются уравнения:

$a(-1)^2+bcdot(-1)+c=0Rightarrow a-b+c=0\a(5)^2+bcdot5+c=0Rightarrow25a+5b+c=0$

Экстремум квадратичной функции находится в точке вершины параболы, через которую проходит её ось симметрии. Координата y=-9, координату x можно найти, как середину отрезка (-1;5):

$x_0=frac{-1+5}2=frac42=2$

То есть, вершина параболы находится в точке O(2; -9). Теперь можно начертить график функции (см.рис.). Координаты точки O также удовлетворяют уравнению параболы:

$a(2)^2+bcdot2+c=-9Rightarrow4a+2b+c=0$

Составим и решим систему уравнений относительно a, b и c:

$begin{cases} a-b+c=0\25a+5b+c=0\4a+2b+c=-9end{cases}Rightarrowbegin{cases} a=b-c\25b-25c+5b+c=0\4b-4c+2b+c=-9end{cases}Rightarrow\Rightarrowbegin{cases} a=b-c\30b-24c=0\6b-3c=-9end{cases}Rightarrowbegin{cases} a=b-c\5b-4c=0\c=2b+3end{cases}Rightarrowbegin{cases} a=b-c\5b-8c-12=0\c=2b+3end{cases}\Rightarrowbegin{cases} a=1\b=-4\c=-5end{cases}$

То есть, уравнение этой функции имеет вид:

$x^2-4x-5=0$