Предмет: Алгебра,
автор: Romanova3
Помогите с решением, пожалуйста
Приложения:
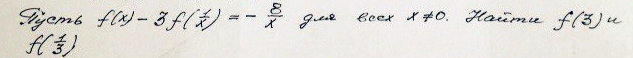
Ответы
Автор ответа:
1
Дано:

Выполним замену переменной

тогда


Поскольку все буквы для обозначения переменных равноправны, то можно последнее равенство написать и так:

Рассмотрим систему двух таких равенств:

Из этой системы найдем
f(x) и f(1/x)

Складываем

Теперь легко найти

Найдем

и

Выполним замену переменной
тогда
Поскольку все буквы для обозначения переменных равноправны, то можно последнее равенство написать и так:
Рассмотрим систему двух таких равенств:
Из этой системы найдем
f(x) и f(1/x)
Складываем
Теперь легко найти
Найдем
и
Похожие вопросы
Предмет: Русский язык,
автор: гейм4
Предмет: Русский язык,
автор: лизaeeer
Предмет: Русский язык,
автор: познаниемира14
Предмет: Математика,
автор: Lily2015