Предмет: Алгебра,
автор: OnHookGames
Решить квадратное неравенство методом интервалов.
Важно решение, а не ответ!Спасибо!
Приложения:
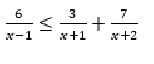
Ответы
Автор ответа:
0
Область определения: x =/= -2, -1, 1
Переносим все налево

Приводим к общему знаменателю

Раскрываем скобки

Упрощаем

Умножим все неравенство на -1, при этом поменяется знак неравенства

Найдем корни числителя


Получаем неравенство

Получаем интервалы:
(-oo; -2); (-2; -5/4]; [-5/4; -1); (-1; 1); (1; 5]; [5; +oo)
По методу интервалов берем какое-нибудь число внутри любого интервала, например, -3, и подставляем:
(-12+5)(-3-5) / [(-3-1)(-3+1)(-3+2)] = (-7)(-8) / [(-4)(-2)(-1)] < 0
Значит, интервал (-oo; -2) не подходит, а подходят следующие интервалы через один: x Є (-2; -5/4] U (-1; 1) U [5; +oo)
Переносим все налево
Приводим к общему знаменателю
Раскрываем скобки
Упрощаем
Умножим все неравенство на -1, при этом поменяется знак неравенства
Найдем корни числителя
Получаем неравенство
Получаем интервалы:
(-oo; -2); (-2; -5/4]; [-5/4; -1); (-1; 1); (1; 5]; [5; +oo)
По методу интервалов берем какое-нибудь число внутри любого интервала, например, -3, и подставляем:
(-12+5)(-3-5) / [(-3-1)(-3+1)(-3+2)] = (-7)(-8) / [(-4)(-2)(-1)] < 0
Значит, интервал (-oo; -2) не подходит, а подходят следующие интервалы через один: x Є (-2; -5/4] U (-1; 1) U [5; +oo)
Похожие вопросы
Предмет: Русский язык,
автор: msabdi
Предмет: Английский язык,
автор: nvv1402
Предмет: Русский язык,
автор: Каролева123
Предмет: Биология,
автор: tsezar7
Предмет: Физика,
автор: Underdog23