Предмет: Алгебра,
автор: aniyn
Решите, пожалуйста.
Надо упростить выражения. Картинка прилагается.
Приложения:
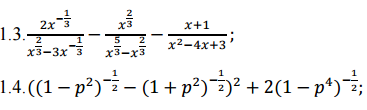
giraffebest:
попробуй на калькуляторе я это не могу решить
На калькуляторе не получится, но спасибо за желание помочь)
Ответы
Автор ответа:
1
Решение смотри в приложении
Приложения:
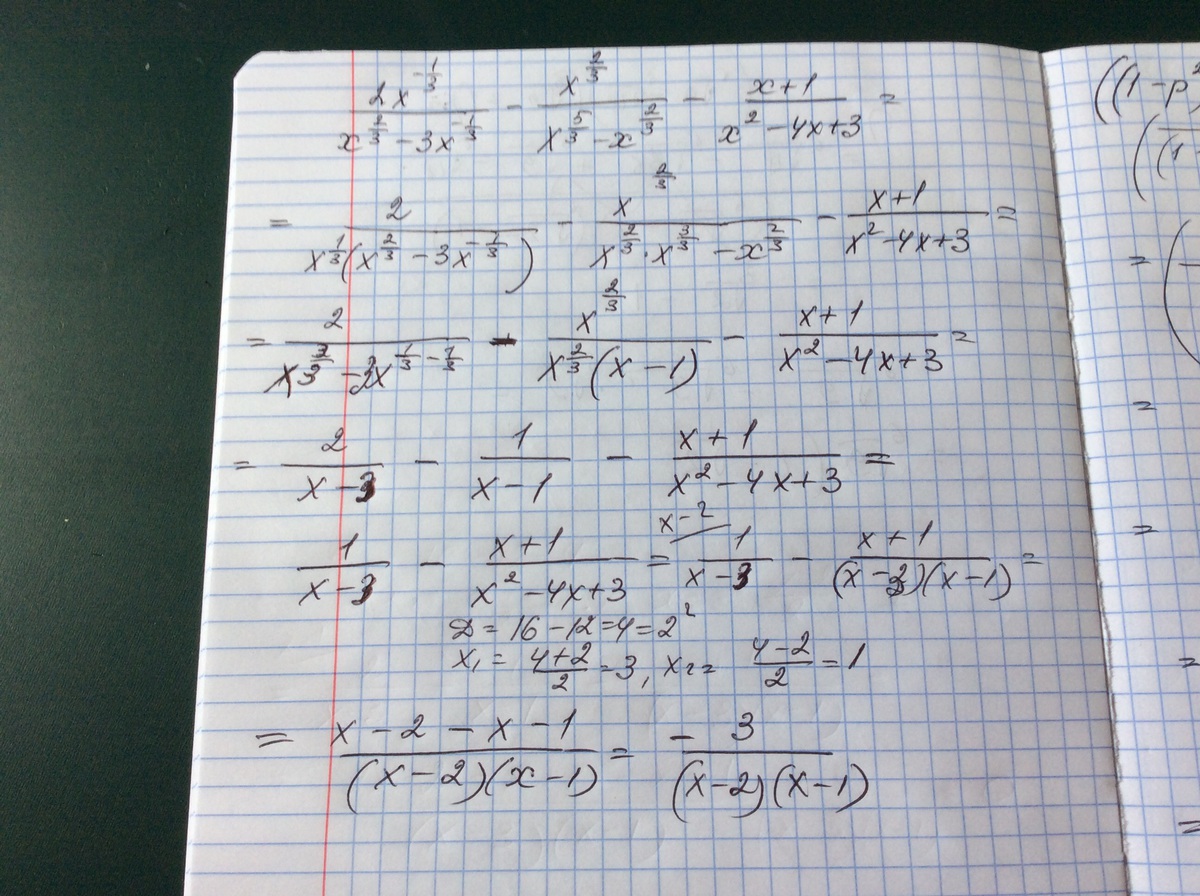
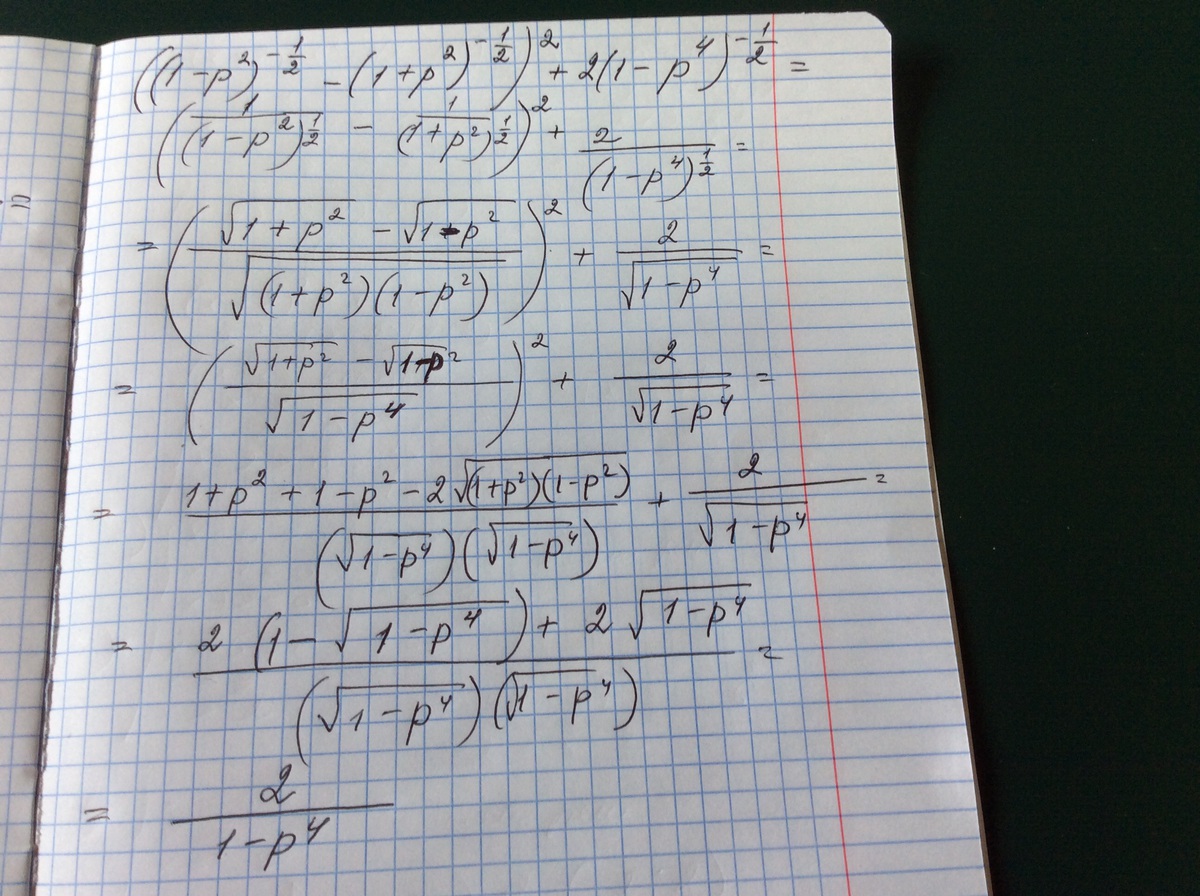
Автор ответа:
0
1.3) 1 дробь домножаем числитель и знаменатель на x^(1/3)

2 дробь тоже домножаем числитель и знаменатель на x^(1/3)

Подставляем все полученное в пример

1.4)




2 дробь тоже домножаем числитель и знаменатель на x^(1/3)
Подставляем все полученное в пример
1.4)
Похожие вопросы
Предмет: Французский язык,
автор: Аноним
Предмет: Русский язык,
автор: fokinairina
Предмет: Қазақ тiлi,
автор: R3ZET
Предмет: Математика,
автор: b1stfox123
Предмет: Математика,
автор: treshMOPS