Предмет: Алгебра,
автор: blacksqur
В первом ответ: x1=pi/4 +pi*n/2; x2=±pi/6+pi*n
Во втором ответ: x1=pi/2 +2p*n; x2=±pi/3+2pi*n
Приложения:
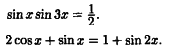
Ответы
Автор ответа:
0
1) 





1.1)
 , k∈Z
, k∈Z
 , k∈Z
, k∈Z
1.2)
 , k∈Z
, k∈Z
 , k∈Z
, k∈Z
2)




2.1)
 , k∈Z
, k∈Z
2.2)
 , k∈Z
, k∈Z
1.1)
1.2)
2)
2.1)
2.2)
Похожие вопросы
Предмет: Русский язык,
автор: рррпрррррррррп
Предмет: Русский язык,
автор: VovkaGamer228
Предмет: Русский язык,
автор: Maksbukin06
Предмет: Геометрия,
автор: slava9232
Предмет: Алгебра,
автор: wanda1265