Предмет: Алгебра,
автор: selecta
Решите пожалуйста модули
Приложения:
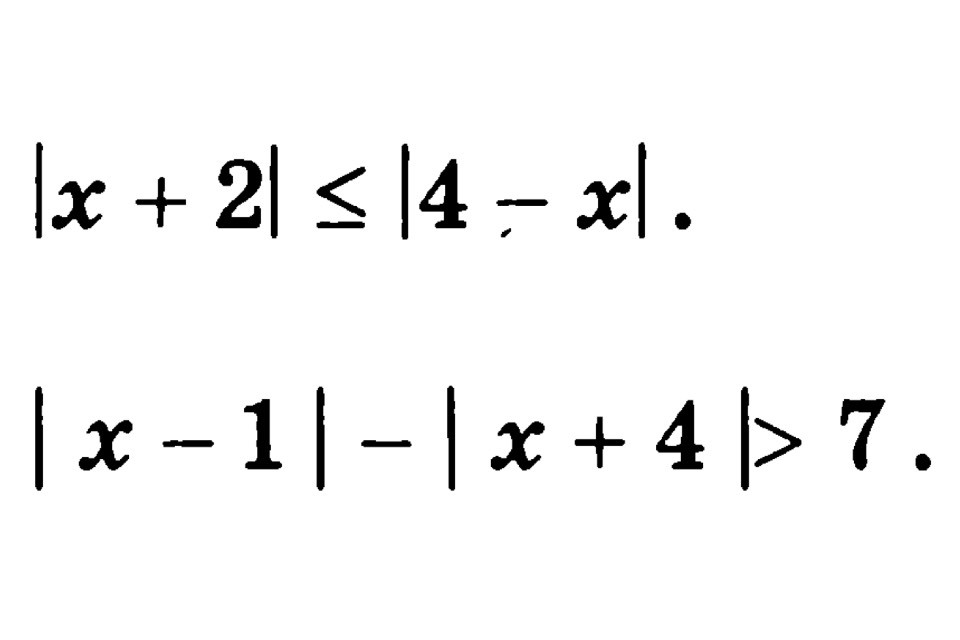
Ответы
Автор ответа:
0
Ix+2I≤I4-xI
Приравниваем подмодульные выражения к нулю:
x=-2 x=4
-∞_________-2_________4_________+∞
x+2 + + +
4-x + + -
Так как на пределах (-∞;-2]U[-2;4], то есть х∈(-∞;4] обе подмодульные выражения положительные ⇒
x+2≤4-x 2x≤2 x≤1.
На пределе x∈[4;+∞) x+2≤-(4-x) 2≤-4, то есть на этом пределе неравенство решения не имеет. ⇒
Ответ: x≤1.
Ix-1I-Ix+4I>7
Приравниваем подмодульные выражения к нулю:
х=1 х=-4
-∞_________-4_________1_________+∞
x+4 - + +
x-1 - - +
x∈(-∞;-4) -(x-1)-(-(x+4)>7 -x+1+x+4>7 5>7 ⇒ x∉
x∈(-4;1) -(x-1)-(x+4)>7 -x+1-x-4>7 x<-6 ⇒ х∉(-4;1)
x∈(1;+∞) x-1-(x+4)>7 x-1-x-4>7 -5>7 ⇒ x∉
Ответ: нет решений.
Приравниваем подмодульные выражения к нулю:
x=-2 x=4
-∞_________-2_________4_________+∞
x+2 + + +
4-x + + -
Так как на пределах (-∞;-2]U[-2;4], то есть х∈(-∞;4] обе подмодульные выражения положительные ⇒
x+2≤4-x 2x≤2 x≤1.
На пределе x∈[4;+∞) x+2≤-(4-x) 2≤-4, то есть на этом пределе неравенство решения не имеет. ⇒
Ответ: x≤1.
Ix-1I-Ix+4I>7
Приравниваем подмодульные выражения к нулю:
х=1 х=-4
-∞_________-4_________1_________+∞
x+4 - + +
x-1 - - +
x∈(-∞;-4) -(x-1)-(-(x+4)>7 -x+1+x+4>7 5>7 ⇒ x∉
x∈(-4;1) -(x-1)-(x+4)>7 -x+1-x-4>7 x<-6 ⇒ х∉(-4;1)
x∈(1;+∞) x-1-(x+4)>7 x-1-x-4>7 -5>7 ⇒ x∉
Ответ: нет решений.
Похожие вопросы
Предмет: Английский язык,
автор: умняшка176
Предмет: Английский язык,
автор: Alypakor
Предмет: Русский язык,
автор: xxxSalavat3
Предмет: Математика,
автор: jdjrjrjrkelrlr