Предмет: Геометрия,
автор: biber450
Площадь прямоугольного треугольника равна(338к3)/3 . Один из острых углов равен 30 . Найдите длину катета, прилежащего к этому углу.
Ответы
Автор ответа:
6
Обозначим катет прилежащий к углу в 30 через a , катет лежащий против угла в 30 или прилежащий к углу в 60 через b. Вычислим площадь этого треугольника по формуле: площадь треугольника равна половине произведения длин двух сторон на синус угла между ними.. Обозначим гипотенузу треугольника через c.
S=a·c·sin30/2
S=b·c·sin60/2,
приравняем эти выражения S=S, a·c·sin30/2=b·c·sin60,
после сокращения: a·sin30=b·sin60, выразим b через a,
b=a·sin30/sin60=a·(1/2)/(√3/2)=a/√3
Вычислим площадь нашего треугольника по формуле: площадь прямоугольного треугольника равна половине произведения его катетов
S= a·b/2, S= a·(a/√3)/2= a²/2√3, S=338√3/3,
338√3/3=a²/2√3, a²=(338·√3·√3·2)/3=338·3·2/3=169·2·2, a=√169·4=13·2·√=26,
сторона а прилежащая к углу в 30 градусов, а= 26.
S=a·c·sin30/2
S=b·c·sin60/2,
приравняем эти выражения S=S, a·c·sin30/2=b·c·sin60,
после сокращения: a·sin30=b·sin60, выразим b через a,
b=a·sin30/sin60=a·(1/2)/(√3/2)=a/√3
Вычислим площадь нашего треугольника по формуле: площадь прямоугольного треугольника равна половине произведения его катетов
S= a·b/2, S= a·(a/√3)/2= a²/2√3, S=338√3/3,
338√3/3=a²/2√3, a²=(338·√3·√3·2)/3=338·3·2/3=169·2·2, a=√169·4=13·2·√=26,
сторона а прилежащая к углу в 30 градусов, а= 26.
Автор ответа:
2
Вариант решения.
Пусть дан треугольник АВС с прямым углом С.
Сумма острых углов прямоугольного треугольника равна 90º.
Угол В=30º,⇒ угол А=60º.
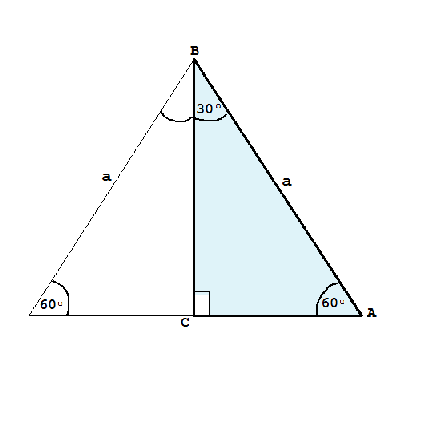
Площадь прямоугольного треугольника с острыми углами 30º и 60º равна половине площади равностороннего треугольника со стороной а.
Площадь правильного треугольника находят по формуле (a²√3):4
Тогда
S Δ ABC=0,5*(a²√3):4=(a²√3):8, где АВ=а.
По условию
(a²√3):8=(338√3):3
3a²=8*338=8*2*169=4²*13²
a²=(4²*13²):3
a=4*13:√3
АВ=4*13:√3
К углу, равному 30º, прилежит катет ВС.
ВС=АВ*cos 30º
BC=(4*13:√3)*√3]:2=26
---
Тот же результат получится, если находить ВС по т. Пифагора, приняв АС за а/2.
Пусть дан треугольник АВС с прямым углом С.
Сумма острых углов прямоугольного треугольника равна 90º.
Угол В=30º,⇒ угол А=60º.
Площадь прямоугольного треугольника с острыми углами 30º и 60º равна половине площади равностороннего треугольника со стороной а.
Площадь правильного треугольника находят по формуле (a²√3):4
Тогда
S Δ ABC=0,5*(a²√3):4=(a²√3):8, где АВ=а.
По условию
(a²√3):8=(338√3):3
3a²=8*338=8*2*169=4²*13²
a²=(4²*13²):3
a=4*13:√3
АВ=4*13:√3
К углу, равному 30º, прилежит катет ВС.
ВС=АВ*cos 30º
BC=(4*13:√3)*√3]:2=26
---
Тот же результат получится, если находить ВС по т. Пифагора, приняв АС за а/2.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: magdi05
Предмет: Русский язык,
автор: leradulova1234
Предмет: Русский язык,
автор: Помогите2282007
Предмет: Математика,
автор: Аноним
Предмет: Физкультура и спорт,
автор: ylek91