Question

1) Радиус шара равен 17 см. Найдите площадь сечения шара, удалённого от его центра на 15 см.

Answer 1

Ответ:   64π см²

Объяснение:

Сечение шара - круг.

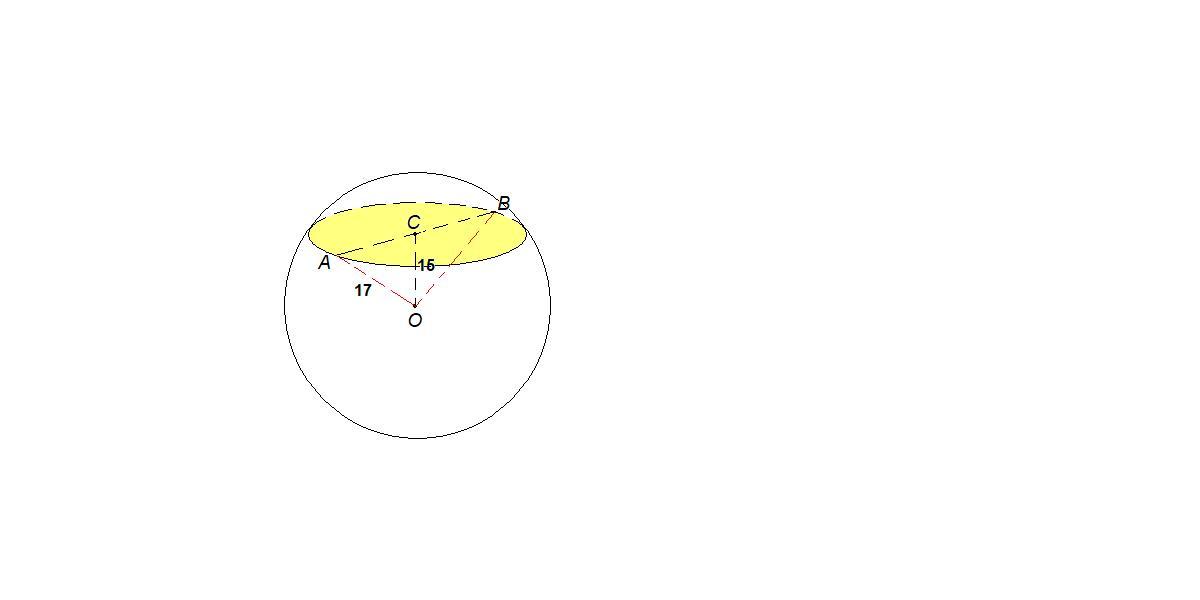
О - центр шара,  С - центр сечения.

Отрезок, соединяющий центр шара с центром сечения, перпендикулярен плоскости сечения, поэтому

ОС = 15 см - расстояние от центра шара до сечения.

ОА = 17 см - радиус шара.

ΔАОС:  ∠АСО = 90°, по теореме Пифагора

            АС = √(ОА² - ОС²) = √(17² - 15²) = √(289 - 225) = √64 = 8 см

Площадь сечения:

S = πr², где r = АС - радиус сечения.

S = π · 8² = 64π см²