Предмет: Алгебра,
автор: Аноним
Решите уравнение:
внутри скрин
Приложения:
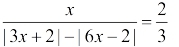
Ответы
Автор ответа:
2
Изучим ОДЗ сперва:
х≠0, так как при нём дробь равна 0 и условие не выполнено ,l3x+2l≠l6x-2l,![\frac{[3x+2]}{[6x-2]} \neq 1; [ \frac{3x+2}{6x-2} ] \neq 1; \left \{ {{ \frac{3x+2}{6x-2} \neq 1 } \atop { \frac{3x+2}{6x-2} \neq -1}} \right. ; \left \{ {{3x+2 \neq 6x-2} \atop {3x+2 \neq -6x+2}} \right.; \left \{ {{-3x \neq -4} \atop {9x \neq 0}} \right.; \left \{ {{x \neq \frac{4}{3} } \atop {x \neq 0}} \right. \frac{[3x+2]}{[6x-2]} \neq 1; [ \frac{3x+2}{6x-2} ] \neq 1; \left \{ {{ \frac{3x+2}{6x-2} \neq 1 } \atop { \frac{3x+2}{6x-2} \neq -1}} \right. ; \left \{ {{3x+2 \neq 6x-2} \atop {3x+2 \neq -6x+2}} \right.; \left \{ {{-3x \neq -4} \atop {9x \neq 0}} \right.; \left \{ {{x \neq \frac{4}{3} } \atop {x \neq 0}} \right.](https://tex.z-dn.net/?f=+%5Cfrac%7B%5B3x%2B2%5D%7D%7B%5B6x-2%5D%7D+%5Cneq+1%3B+%5B+%5Cfrac%7B3x%2B2%7D%7B6x-2%7D+%5D+%5Cneq+1%3B++%5Cleft+%5C%7B+%7B%7B+%5Cfrac%7B3x%2B2%7D%7B6x-2%7D+%5Cneq+1+%7D+%5Catop+%7B+%5Cfrac%7B3x%2B2%7D%7B6x-2%7D+%5Cneq+-1%7D%7D+%5Cright.+%3B+%5Cleft+%5C%7B+%7B%7B3x%2B2+%5Cneq+6x-2%7D+%5Catop+%7B3x%2B2+%5Cneq+-6x%2B2%7D%7D+%5Cright.%3B+%5Cleft+%5C%7B+%7B%7B-3x+%5Cneq+-4%7D+%5Catop+%7B9x+%5Cneq+0%7D%7D+%5Cright.%3B+%5Cleft+%5C%7B+%7B%7Bx+%5Cneq++%5Cfrac%7B4%7D%7B3%7D+%7D+%5Catop+%7Bx+%5Cneq+0%7D%7D+%5Cright.++)
Теперь решаем само уравнение по свойству пропорции
![3x=2([3x+2]+[6x-2]); 3x=2[3x+2]+2[6x-2]; 3x=2([3x+2]+[6x-2]); 3x=2[3x+2]+2[6x-2];](https://tex.z-dn.net/?f=3x%3D2%28%5B3x%2B2%5D%2B%5B6x-2%5D%29%3B+3x%3D2%5B3x%2B2%5D%2B2%5B6x-2%5D%3B) теперь находим нуль каждого модуля и смотрим, на каких промежутках с какими знаками их надо раскрывать.
теперь находим нуль каждого модуля и смотрим, на каких промежутках с какими знаками их надо раскрывать.  ,
,
- + +
--------------------------------------------------------------------------------------------------->
- -2/3 - 1/3 +
Верхний знак - знак раскрытия модуля [3x+2] на промежутке, нижний - [6x-2]
Рассматриваем 3 случая:
1) ;
;  - принадлежит этому промежутку;
- принадлежит этому промежутку;
2) ;
;  - не подходит по ОДЗ
- не подходит по ОДЗ
3) ;
;  - не принадлежит рассматриваемой области, таким образом, корень всего один:
- не принадлежит рассматриваемой области, таким образом, корень всего один:  . Ответ:
. Ответ:  .
.
х≠0, так как при нём дробь равна 0 и условие не выполнено ,l3x+2l≠l6x-2l,
Теперь решаем само уравнение по свойству пропорции
- + +
--------------------------------------------------------------------------------------------------->
- -2/3 - 1/3 +
Верхний знак - знак раскрытия модуля [3x+2] на промежутке, нижний - [6x-2]
Рассматриваем 3 случая:
1)
2)
3)
Похожие вопросы
Предмет: Окружающий мир,
автор: Nooble1234567890
Предмет: Русский язык,
автор: lifeminelivegood
Предмет: Русский язык,
автор: darya110606
Предмет: Геометрия,
автор: Nasya8888
Предмет: Английский язык,
автор: snnansns