Предмет: Алгебра,
автор: КсюшаМК
Помогите решить, пожалуйста: 5) lg^2(9000)*log3(10)-((3-lg9)^2/lg3)
Приложения:
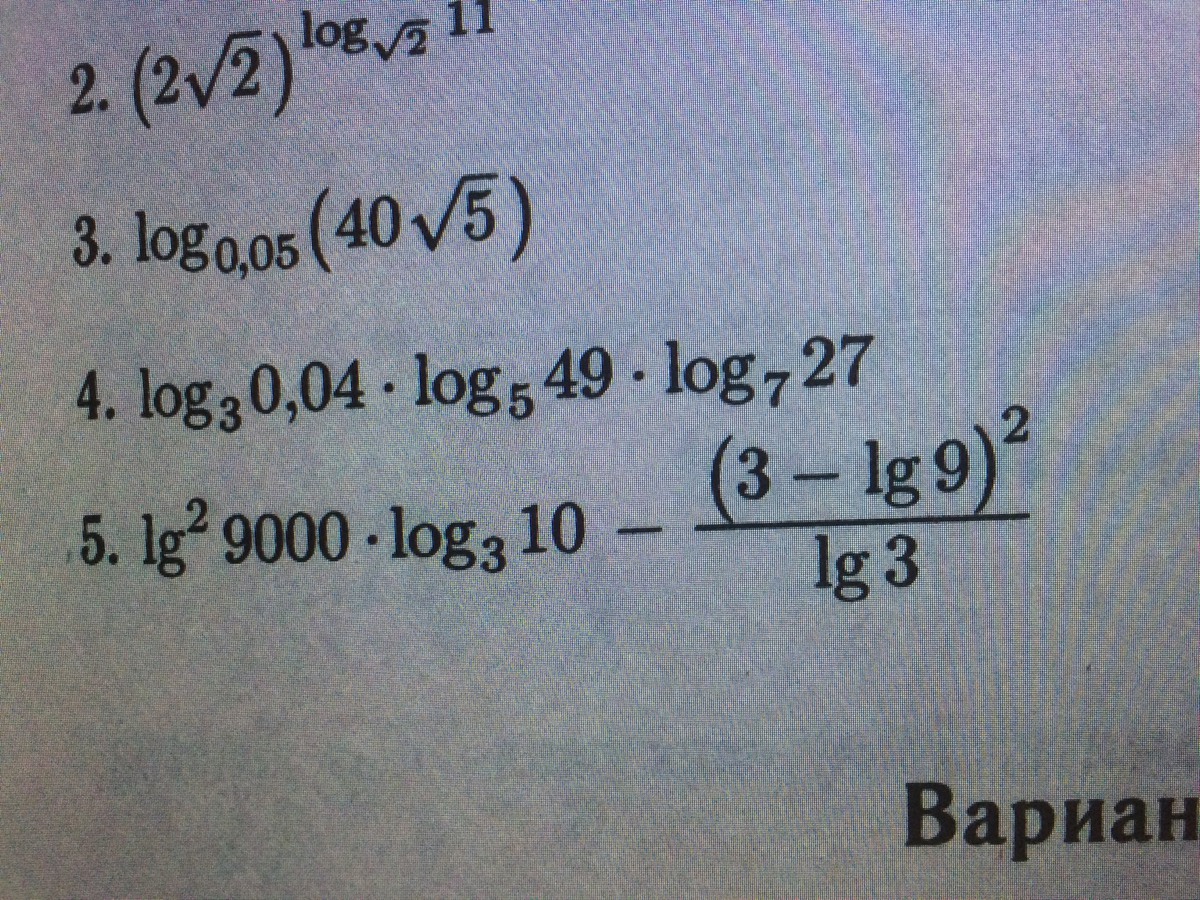
Ответы
Автор ответа:
4
Приложения:
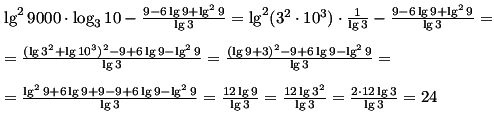
КсюшаМК:
должно получиться 24 :с
Получилось 24:)
У вас отображается текст формулы?
а, видимо, с телефона что-то не так, спасибо! открою с компа
Я приложу фото, обновите страницу)
хорошо, благодарю)
Автор ответа:
0
Смотреть во вложении
Приложения:
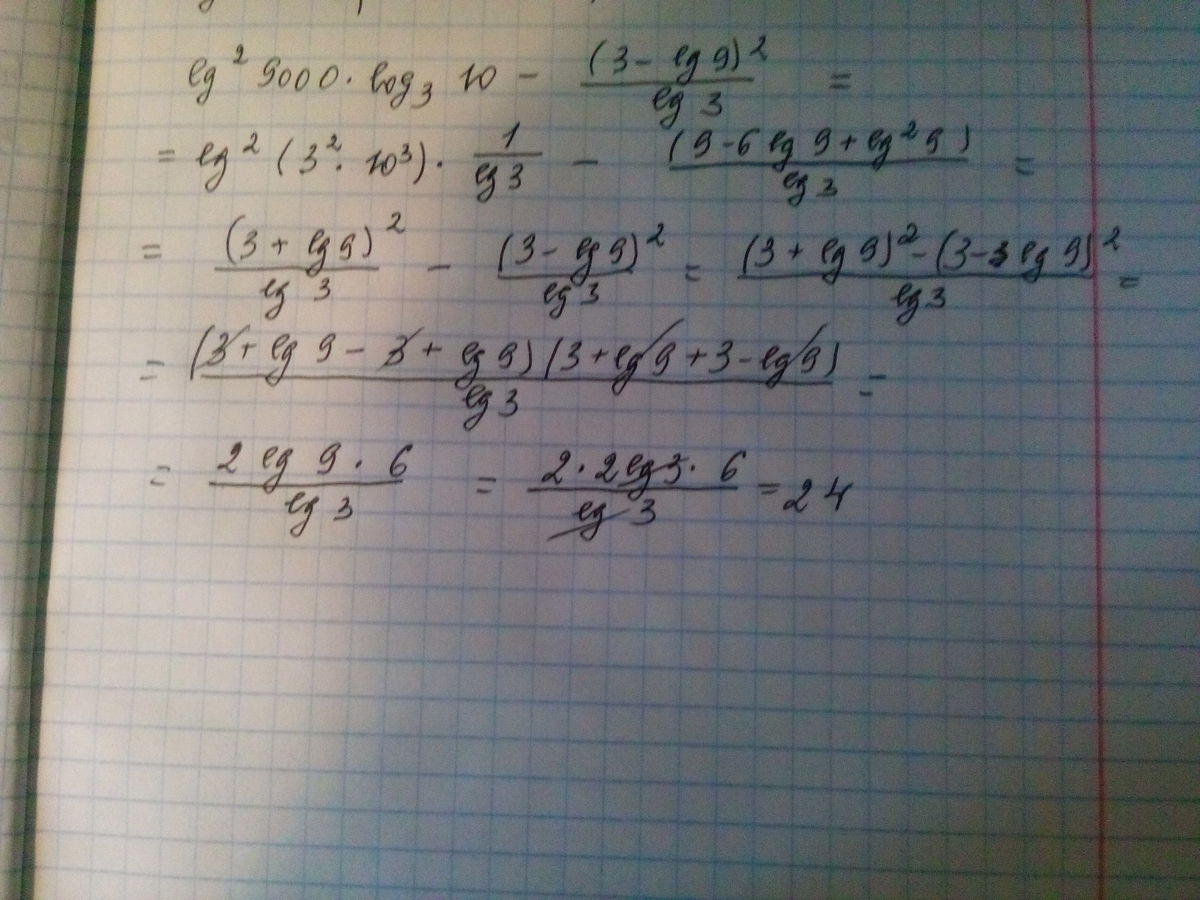
Похожие вопросы
Предмет: Русский язык,
автор: vasia33
Предмет: Русский язык,
автор: ars444555
Предмет: Русский язык,
автор: Аноним
Предмет: Физика,
автор: daniillihvan
Предмет: Русский язык,
автор: selina2372