Question

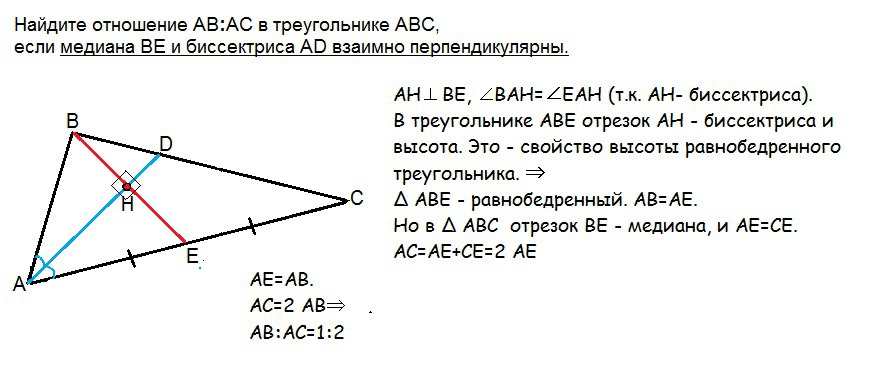
Найдите отношение AB:AC в треугольнике ABC, если медиана BE и биссектриса AD взаимно перпендикулярны.

Answer 1

Обозначим точку пересечения ВЕ и AD буквой Н. 
АН⊥ВЕ, ∠ВАН=∠ЕАН (АН- биссектриса). 
В треугольнике АВЕ отрезок АН - биссектриса и высота. Это - свойство высоты равнобедренного треугольника. ⇒ 
∆ АВЕ - равнобедренный. АВ=АЕ. 
Но в ∆ АВС  отрезок ВЕ - медиана, и АЕ=СЕ. 
АС=АЕ+СЕ=2 АЕ
АЕ=АВ.
АС=2 АВ⇒
АВ:АС=1:2