Предмет: Информатика,
автор: PitMeningit78
Сколько различных вариантов решений имеет уравнение?
(O->L)&(K->L)&(M->!(N))&(L->M)&(M->K)=1
где K, L, M, N, O - логические переменные.
У меня получилось решить методом перебора, но хотелось бы узнать какой-то более правильный способ решения.
Аноним:
Например, провести упрощение выражения и потом посмотреть, какие наборы переменных дают значение 1.
В результате получится KLM!N & !K!L!M!O=1, т.е. 4 варианта
Простите, а можно подробный ход решения.
Там очень много писать... почти целый лист А4, а уж набирать это в редакторе за 5 баллов просто неприлично))))
:(
Ответы
Автор ответа:
2
Верно написано, что 4 решения.
см. прикрепленные файлы.
см. прикрепленные файлы.
Приложения:
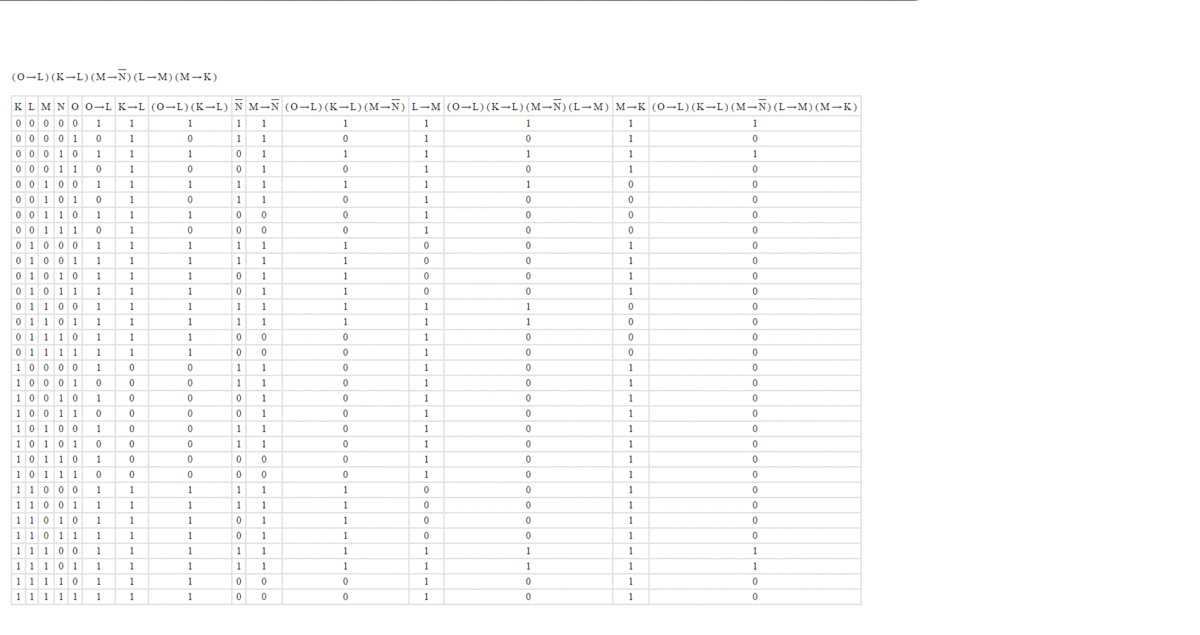

Ой....какой вывод гигантский, хорошо хоть, что не вручную сделан)))
Автор ответа:
1
Для удобства записи перепишем условие в несколько иную систему обозначений (но тоже вполне легальную)
Левая часть полученного выражения истинна, если истинна хотя бы одна из двух конъюнкций. Каждая из этих конъюнкций не включает одну из пяти переменных, следовательно, она не зависит от значения этой переменной и дает истинность как при ложном, так и при истинном её значении.
Итого получается ЧЕТЫРЕ различных варианта решения.
Спасибо огромное
:)
Похожие вопросы
Предмет: Английский язык,
автор: barinovaYI
Предмет: Окружающий мир,
автор: dkhairov1993
Предмет: Русский язык,
автор: samira9992
Предмет: Математика,
автор: lolitayn
Предмет: Английский язык,
автор: bondarenkoneki