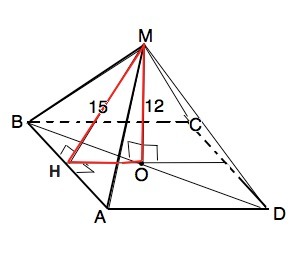
Помогите пожалуйста: В правильной четырехугольной пирамиде высота равна 12 см, а высота боковой грани -15 см. Найдите боковое ребро.
Ответы
Правильная четырехугольная пирамида — это многогранник, у которого основание пирамиды — квадрат, а боковые грани — равные равнобедренные треугольники. Высота опускается в центр пересечения диагоналей квадрата основания из вершины.
Пусть данная пирамида МАВСD. МО - высота, МН - высота боковой грани ( апофема). Высота МН равнобедренного ∆ ВМА - его медиана. ВН=АН.
МО перпендикулярна плоскости основания и потому перпендикулярна любой прямой, лежащей в этой плоскости и проходящей через О.
∆ МОН - прямоугольный. Это "египетский" треугольник с отношением катета и гипотенузы 4:5, следовательно, ОН=9 ( то же получим и по т.Пифагора).
ОН по т. о 3-х перпендикулярах перпендикулярна АВ, следовательно, треугольник ВОН - прямоугольный равнобедренный ВН=ОН. ВО=ОН√2=9√2.
По т.Пифагора ВМ=√(МО²+BО²)=√(144+162)=√306=3√34