Предмет: Алгебра,
автор: Исповедница
Очень важно! Не могу понять! Содержание задачи: Один из катетов прямоугольного треугольника больше другого катета на 14 см и меньше гипотенузы на 2 см. Найдите периметр этого треугольника!
Ответы
Автор ответа:
0
Пусть больший из катетов равен х см, тогда второй катет равен х-14 см, а гипотенуза равна х+2 см. За теоремой Пифагора составляем уравнение:
так как 8-14=-6 , а длина катета положительное число, то
больший катет равен 24 см, меньший катет равен 24-14=10 см, а гипотенуза рава 24+2=26 см
Периметр - сумма всех сторон.
Периметр данного треугольника равен 24+10+26=60 см
ответ: 60 см
Автор ответа:
0
всеееееееееееееееееееееее
Приложения:
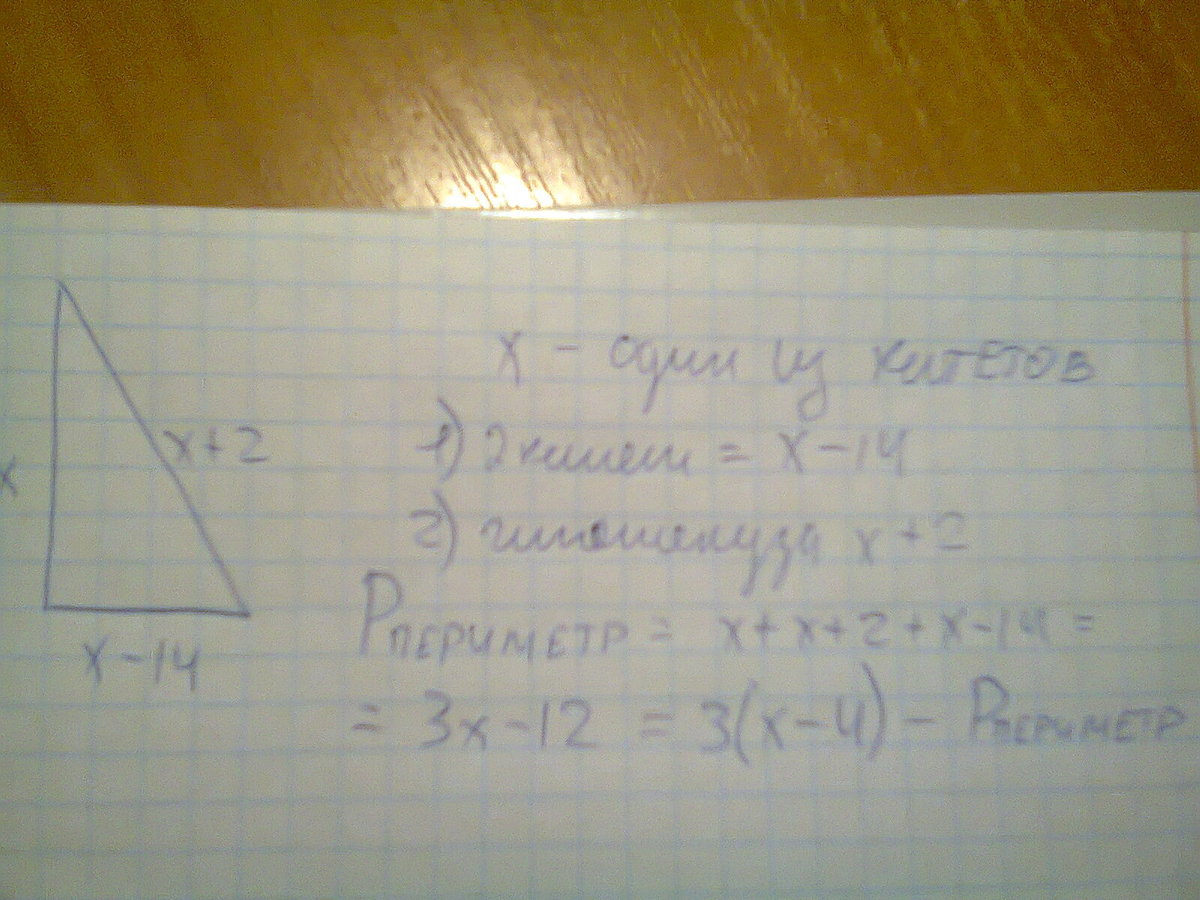
Похожие вопросы
Предмет: Алгебра,
автор: mmmakm
Предмет: Математика,
автор: raniaryskali
Предмет: Русский язык,
автор: alexgavrilovamy
Предмет: Алгебра,
автор: MиLаХа
Предмет: Алгебра,
автор: malikasautova95