Предмет: Алгебра,
автор: Nadmitr56
срочно нужно решить Помогите пожалуйста
Приложения:
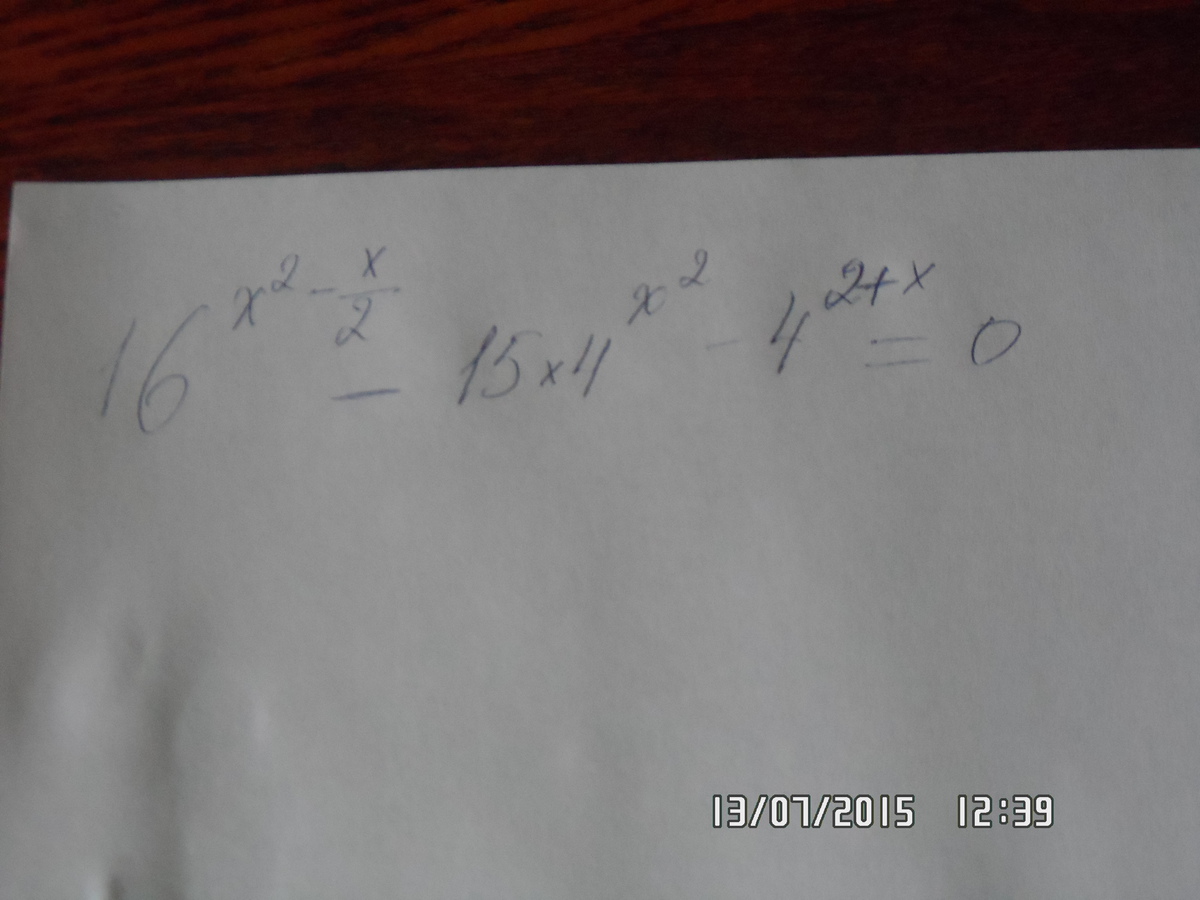
ВладимирБ:
в условии все верно?
Ответы
Автор ответа:
2
Это однородное уравнение вида
au²+buv+cv²=0
Решается делением на u²≠0 или v²≠0
получается квадратное уравнение
at²+bt+c=0, t=u/v

![(4^{ x^{2}}) ^{2} -15\cdot (4 ^{ x^{2} })\cdot 4 ^{x} -16\cdot (4^{x}) ^{2} =0 [u=4 ^{ x^{2} };v =4 ^{x}] \\ \\ t ^{2}-15t-16=0, \\ \\ t= \frac{4 ^{ x^{2} } }{4 ^{x} } (4^{ x^{2}}) ^{2} -15\cdot (4 ^{ x^{2} })\cdot 4 ^{x} -16\cdot (4^{x}) ^{2} =0 [u=4 ^{ x^{2} };v =4 ^{x}] \\ \\ t ^{2}-15t-16=0, \\ \\ t= \frac{4 ^{ x^{2} } }{4 ^{x} }](https://tex.z-dn.net/?f=%284%5E%7B+x%5E%7B2%7D%7D%29+%5E%7B2%7D++-15%5Ccdot+%284+%5E%7B+x%5E%7B2%7D+%7D%29%5Ccdot+4+%5E%7Bx%7D++-16%5Ccdot+%284%5E%7Bx%7D%29+%5E%7B2%7D+%3D0+%5Bu%3D4+%5E%7B+x%5E%7B2%7D+%7D%3Bv+%3D4+%5E%7Bx%7D%5D+%5C%5C++%5C%5C+t+%5E%7B2%7D-15t-16%3D0%2C+%5C%5C++%5C%5C+t%3D+%5Cfrac%7B4+%5E%7B+x%5E%7B2%7D+%7D+%7D%7B4+%5E%7Bx%7D+%7D+++++)
t₁=(15+17)/2=16 или t₂=(15-17)/2=-1
 или
или 

корни х₁=2 х₂=-1
tex]4 ^{ x^{2} -x}=-1 [/tex]
это уравнение не имеет корней, так как показательная функция принимает только положительные значения.
Ответ. -1 ; 2
au²+buv+cv²=0
Решается делением на u²≠0 или v²≠0
получается квадратное уравнение
at²+bt+c=0, t=u/v
t₁=(15+17)/2=16 или t₂=(15-17)/2=-1
корни х₁=2 х₂=-1
tex]4 ^{ x^{2} -x}=-1 [/tex]
это уравнение не имеет корней, так как показательная функция принимает только положительные значения.
Ответ. -1 ; 2
Похожие вопросы
Предмет: Русский язык,
автор: olga4534200
Предмет: Английский язык,
автор: почем12345
Предмет: Русский язык,
автор: света938
Предмет: Математика,
автор: necitvezunchic
Предмет: Қазақ тiлi,
автор: milki1538