Предмет: Математика,
автор: 12pt12
Решите логарифмическое неравенство и укажите его наибольшее значение
Приложения:
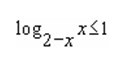
Ответы
Автор ответа:
1
ОДЗ данного неравенства:
{2-x>0
{x>0
{2-x≠1
или
{x<2
{x>0
{x≠1
(0;1)U(1;2)
Данное неравенство эквивалентно следующим неравенствам
{x>0 {x>0
{2-x>1 ⇔ {x<1
{x ≤ 2-x {x≤1
Решение данной системы неравенств является интервал (0;1)
и
{x>0 {x>0
{0<2-x<1 ⇔ {1<x<2
{x≥2-x {x≥1
Решением данной системы неравенств является интервал(1;2)
Поэтому исходное неравенство имеет решения для всех
значений х ∈(0;1)U(1;2)
Ответ:(0;1)U(1;2)
Легко доказать что исходное неравенство истинно на всей области его определения или что
для всех
значений х ∈(0;1)U(1;2)
так как
В данной дроби числитель при значении х∈(0;1) отрицателен, а при значении х∈(1;2) положителен.
Знаменатель наоборот при при значении х∈(0;1) положителен, а при значении х∈(1;2) отрицателен. Поэтому значение дроби для всех значений х∈(0;1)U(1;2) всегда меньше нуля. Раз данный логарифм при всех значениях х∈(0;1)U(1;2) меньше нуля то следовательно и меньше 1.
Наибольшего целого значения решения неравенства нет.
Похожие вопросы
Предмет: Английский язык,
автор: Grace36912
Предмет: Русский язык,
автор: amina322
Предмет: Русский язык,
автор: знакомьтесь
Предмет: Математика,
автор: shugyla6183
Предмет: Математика,
автор: nurda777nurik