Предмет: Геометрия,
автор: Ranger2001
длины сторон треугольника относятся как 5:4:3. найдите отношение длин отрезков сторон на которые они делятся точками касания вписанной окружности
Ответы
Автор ответа:
1
Треугольник, в котором длины сторон относятся как 5:4:3 - прямоугольный "египетский". Радиус прямоугольного треугольника можно найти по формуле:
r=(a+b-c):2, где а и b- катеты, с- гипотенуза треугольника.
r=(4+3-5):2=1
Рассмотрим рисунок.
Длины отрезков касательных до точки касания, проведенных из одной точки, равны.
ТС=СН=r=1
ВН=ВМ=3-1=2
АТ=АМ=4-1=3 ⇒
СН::НВ=1:2
СТ:ТА=1:3
ВМ:МА=2:3
Искомое отношение длин отрезков равно 1:2:3
r=(a+b-c):2, где а и b- катеты, с- гипотенуза треугольника.
r=(4+3-5):2=1
Рассмотрим рисунок.
Длины отрезков касательных до точки касания, проведенных из одной точки, равны.
ТС=СН=r=1
ВН=ВМ=3-1=2
АТ=АМ=4-1=3 ⇒
СН::НВ=1:2
СТ:ТА=1:3
ВМ:МА=2:3
Искомое отношение длин отрезков равно 1:2:3
Приложения:
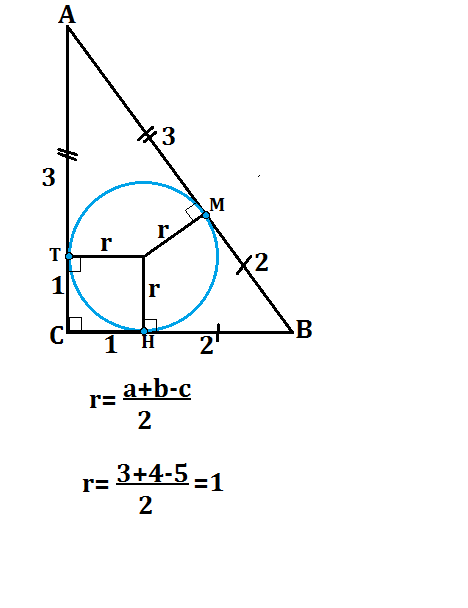
Похожие вопросы
Предмет: Қазақ тiлi,
автор: гульнар20091
Предмет: Русский язык,
автор: Albina0981
Предмет: Английский язык,
автор: emartynov75
Предмет: Английский язык,
автор: lakapova2