Предмет: Алгебра,
автор: oihgsgjs
Решите неравенство, пожалуйста, подробно.
Ответ: [0; 3]; (5; 6)
Приложения:
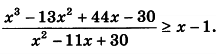
Ответы
Автор ответа:
4
решаем методом интервалов: наносим на числовую прямую точки x=0 и x=3 - закрашенные, а x=5 и x=6 - выколотые
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: kirilmihaylov20
Предмет: Русский язык,
автор: Verik555
Предмет: Русский язык,
автор: Цаприка
Предмет: ОБЖ,
автор: Аноним
Предмет: Английский язык,
автор: tatyana8011988