Question

Найдите наибольшее значение функции y=3x-sqrt(9x^2-6x+1)-sqrt(4x^2-12x+9)

Answer 1

y=3x-√(9x²-6x+1) -√(4x²-12x+9)=3x -√(3x-1)² - √(2x-3)² =3x-|3x-1|-|2x-3|
y=3x-|3x-1|-|2x-3|.

Нули подмодульных выражений:
3x-1=0
3x=1
x=1/3

2x-3=0
2x=3
x=1.5

Вершины ломаной:
x=1/3      y=3*(1/3) - |3*(1/3)-1|-|2*(1/3)-3|=1-|1-1|-|2/3 - 3|=1-|-7/3|=1-7/3
                = -4/3= -1 ¹/₃
(¹/₃; -1 ¹/₃) - первая вершина.

х=1,5     у=3*1,5-|3*1.5-1|-|2.*1.5-3|=4.5-|3.5|-|0|=1
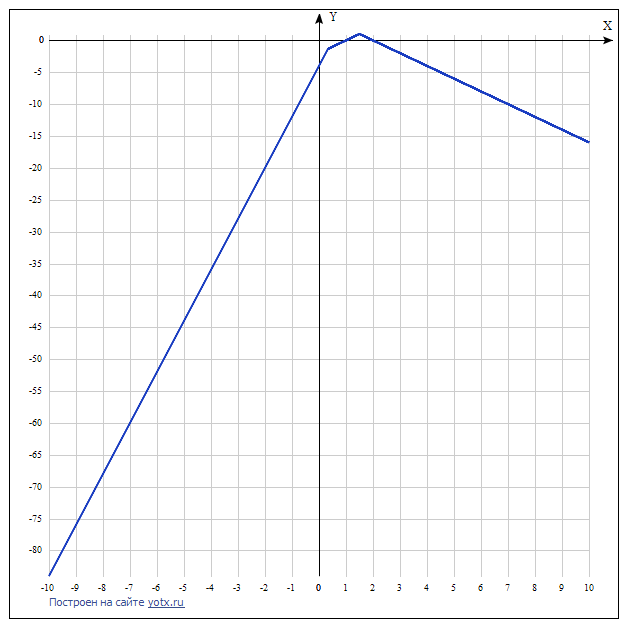
(1.5; 1) - вторая вершина.

Контрольные точки ломаной:
х=-2       у=3*(-2) - |3*(-2)-1| - |2*(-2)-3| =
               = -6 - |-7| - |-7| = -6 -7 -7 =-20
(-2; -20) - первая контрольная точка слева.

х=4      у=3*4 - |3*4-1| - |2*4-3| =12 - |11| - |5|=12-11-5=-4
(4; -4) - вторая контрольная точка справа.

Наибольшее значение функции у=1.
Ответ: 1.