Предмет: Алгебра,
автор: Totalkol2
Найти все целые числа для которых:
Приложения:
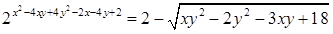
Ответы
Автор ответа:
0
Скорее всего в показателе слева опечатка, там должно быть +4y, а не -4y. Тогда x²-4xy+4y²-2x+4y+2=(x-2y-1)²+1, т.е. он всегда ≥1, поэтому вся левая часть ≥2. Правая часть всегда ≤2. Значит равенство может быть только если x=2y+1, и выражение под корнем =0.
Т.к. xy²-2y²-3xy+18=(y-3)(y(x-2)-6)=(y-3)(2y²-y-6)=(y-3)(y-2)(2y+3), то получаем три решения (7;3), (5;2), (-2;-3/2).
Т.к. xy²-2y²-3xy+18=(y-3)(y(x-2)-6)=(y-3)(2y²-y-6)=(y-3)(y-2)(2y+3), то получаем три решения (7;3), (5;2), (-2;-3/2).
Похожие вопросы
Предмет: Английский язык,
автор: Poltos1
Предмет: Русский язык,
автор: Anna13112008
Предмет: Русский язык,
автор: gordyuta01
Предмет: Алгебра,
автор: sofaborisova87200
Предмет: Алгебра,
автор: ФэшэнЛЕДИ