Предмет: Математика,
автор: igorartemych
Помогите пожалуйста
Найдите значения других трех основных тригонометрических функций, если
Приложения:
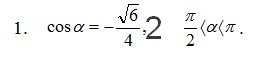
Ответы
Автор ответа:
1
sina=√(1-cos²a)=√(1-6/16)=√(10/16)=√10/4
tga=sina/cosa=√10/4:(-√6)/4=-√10/4*4/√6=-√(10/6)=-√15/3
ctga=1/tga=1:(-√15/3)=-√15/5
tga=sina/cosa=√10/4:(-√6)/4=-√10/4*4/√6=-√(10/6)=-√15/3
ctga=1/tga=1:(-√15/3)=-√15/5
Автор ответа:
2
Основное тригонометрическое тождество 

Похожие вопросы
Предмет: Русский язык,
автор: mariaromanp2crqz
Предмет: Окружающий мир,
автор: Lena11kor
Предмет: Окружающий мир,
автор: вадим20075
Предмет: Физика,
автор: xcxborya1703
Предмет: Математика,
автор: ayten1307