Question

В параллелограмме ABCD окружность, описанная около треугольника АBD, касается прямой СВ. Найдите площадь параллелограмма, если (угол АВС =
$\frac{3 \pi }{4}$ , ВD = 2.

Answer 1

В параллелограмме сумма углов при одной стороне равна 180º.
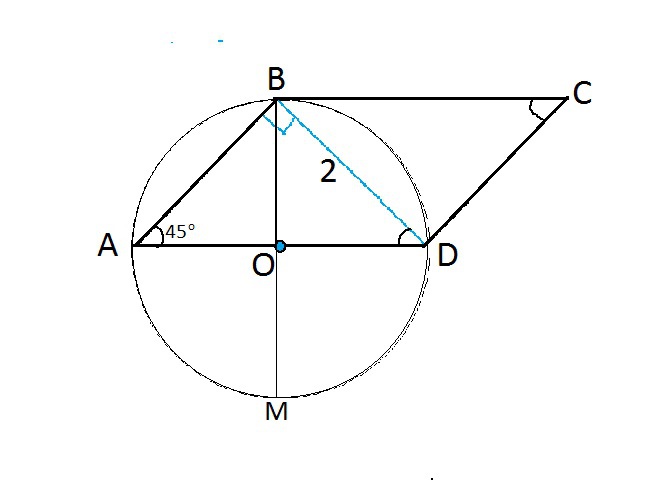
3π/4=135º, следовательно, острый угол параллелограмма равен 45º.
Треугольник АВD- вписанный, точки А, В и D лежат на окружности. Следовательно, точка В является точкой касания, т.к. в противном случае окружность имела бы с касательной (прямой ВС)  две общие точки, что противоречит определению касательной. 
Тогда  ВМ , проведенный в точку касания - диаметр описанной окружности. 
Угол OВС=90º,  АВО=45º.⇒ угол АОВ=90º
Хорда АD  параллельна ВС и потому перпендикулярна диаметру ВМ. Хорда, перпендикулярная диаметру, делится им пополам. Прямоугольные треугольники АВО и ВDO равны по равным катетам, следовательно, угол ВDО=ВАО=45º, угол АВО=45º, OBD=45º, ⇒ угол ABD= 90º. ⇒ угол ВDС=90º
Треугольник АВД равнобедренный прямоугольный, ВD - перпендикулярна  и равна АВ и DC, и является высотой параллелограмма. 
S (ABCD)=BD*DC=2*2=4 (ед. площади)