Предмет: Алгебра,
автор: Arinis
Решите пожалуйста неравенство, у меня не получается
Приложения:
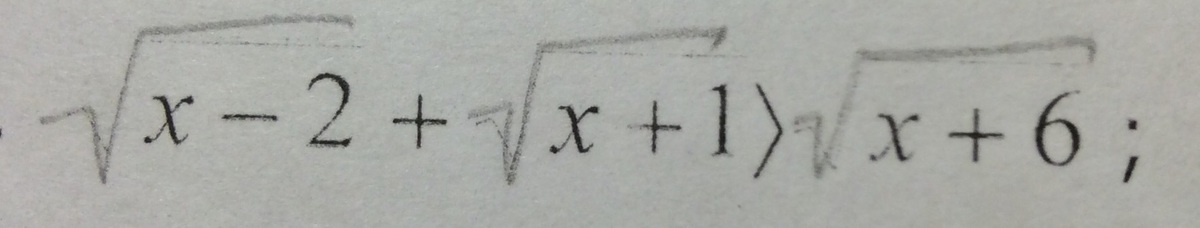
Ответы
Автор ответа:
1
Решение смотри во вложении...
Приложения:
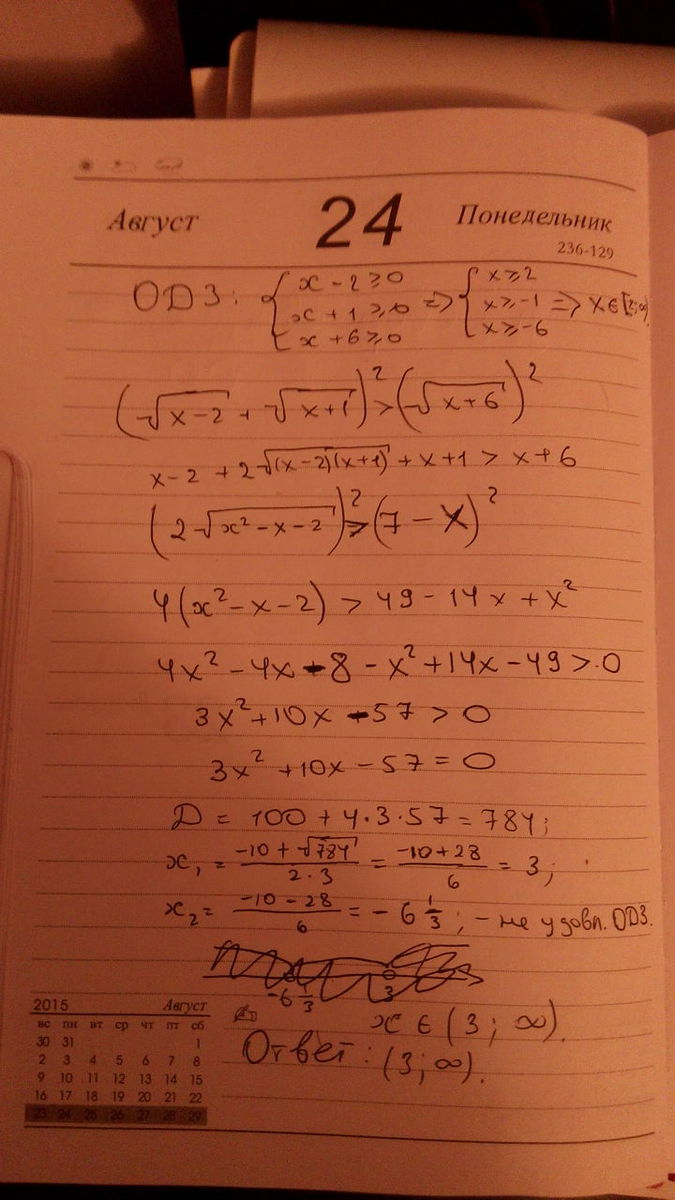
Автор ответа:
1
Рассмотрим функцию
Найдем область определения функции(объяснение как искать: подкоренное выражение должен иметь положительное значение)
Область определения функции:
Приравниваем функцию к нулю:
Возведем обе части в квадрат
Опять же возведем в квадрат
Находим дискриминант
Находим решение неравенства(для начала область определения, ну и потом нули функции)
[2]___-__(3)____+___>
Решение неравенства x>3
Окончательный ответ:
Похожие вопросы
Предмет: Английский язык,
автор: KatyaEgorovaTyan
Предмет: Русский язык,
автор: Zeruhetta
Предмет: Русский язык,
автор: Zeruhetta
Предмет: Английский язык,
автор: saeee
Предмет: История,
автор: Tatarv343